 |
Heute kaum noch vorstellbar -
allein der Krach, die Arbeitsgeschwindigkeit, aber auch der benötigte Strom,
um solche Schaltungen effektiv zu betreiben. Und doch waren die ersten
Computer mit genau den folgend aufgeführten Bauelementen ausgestattet. ausgestattet. |
 |
|
Mechanische Logik |
Grundlagen der Relaisschaltungen |
Grundlagen der Röhrenschaltungen |
TTL-Schaltkreise können eine Lösung sein,
wenn man noch über 'ne "Bastelkiste" verfügt (... aber wer hat so etwas 2009
schon noch???) ;-) |
CMOS-Bauelemente sind auch 2009 in
relativer Vollständigkeit am Markt |
C-Control - leider sehr alt |
|
Zusebleche |
Logik mit Relais |
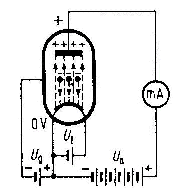
Röhrenschaltungen |
TTL-Liste
Liste meiner "Lieblings"-TTL-Digitalschaltkreise:
7400, 7402, 7404, 7408, 7410, 7411, 7414, 7420, 7427, 7430 |
CMOS-Liste
Liste meiner "Lieblings"-CMOS-Digitalschaltkreise:
4000,
4002, 4009,
4011, 4012,
4023, 4049,
4072,
4073 |
Steuerungstechnik
|
|
|
|
|
|
Fakten werden mit Bedingungen verbunden
und ergeben Ausgangssignale |
Darstellungen der Fakten und Bedingungen |
Fakten:
- typischerweise besitzen die Fakten zwei Schaltzustände -
prinzipiell sind mehr möglich (... drei ganz einfach - mehr mit
Aufwand - nicht an der Technik, sondern am Denken!!!)
- das können Personen mit Namen sein mit Zuständen, welche sie
einnehmen können
- das können schaltbare Komponenten technischer Geräte sein
- in der Technik werden sie mit xIndex bezeichnet also
beispielsweise x3 x2 x1 x0
- die Aufzählung der Fakten ist theoretisch beliebig - praktischer
ist die Darstellung mit der kleinstmöglichen Stelle von rechts
- aus Anzahl der Fakten sowie ihren möglichen logischen Zuständen
ergeben sich Schaltkombinationen
- die Ausgangssignale sind ebenfalls Gerätekomponenten mit
prinzipiell zwei Schaltzuständen - mehr sind möglich
- in der Technik werden sie mit yIndex bezeichnet also
beispielsweise y3 y2 y1 y0
- UND-Funktion wird in der Notation weggelassen (wenn Darstellung
eindeutig!) - ODER muss geschrieben werden
- negierter Zustand wird in binärer Logik mit Überstreichung
dargestellt
- die realen Fakten können Schalter oder Sensoren eines Gerätes sein
- im behandelten Fällen auf zwei Zustände begrenzt - mehr möglich
Zustände machen die Logik extrem viel komplexer - sie bleibt aber
lösbar
|
Bedingungen:
- dies sind streng genommen nur drei Worte, mit denen man durch ihre
gegenseitige Verknüpfung sowie Vorrangautomatik ganze "Computer"
beschreiben kann
- UND - ODER - NICHT - das war's schon - damit "baut" man bis heute und
auf absehbare Zeit hin, Computer
- UND (AND) - geschrieben: ˄
- ODER(OR) - geschrieben: ˅
- NICHT (NOT) - geschrieben: ̅x1 (gelesen:
"Nicht x1")
- daneben werden bedingt durch ihre häufige Anwendung weitere
"Grundfunktionen" als Baustein realisiert - diese könnten aber auch durch
Kombinieren der Basisfunktionen zusammengestellt werden
|
y1= (x0˄ ̅x1 ˄ ̅x2
˄ ̅x3) ˅ (x0 ˄ ̅x1 ˄ x2 ˄ ̅x3
) ˅ ( x0 ˄ x1 ˄ x2 ˄ ̅x3) ˅ ( ̅x0
˄ ̅x1 ˄ x2 ˄ x3)
y0= ( x0 ˄ x1 ˄ ̅x2
˄ ̅x3) ˅ ( ̅x0 ˄ x1 ˄ ̅x2 ˄ x3)
˅ ( x0 ˄ x1 ˄ x2 ˄ x3) |
|
|
|
|
|
Achtung: die
Aufgabenstellung entspricht exakt der unter 1. formulierten Zielstellung -
die Lösung jedoch sieht komplett anders aus!!!
Die Problembeschreibung sowie auch die Lösungsstrategie ist hier nun im
Verfahren enthalten und wenn die entsprechende Software verfügbar ist, ist
die Entwicklung der Logik theoretisch gar kein Problem mehr (fehlerfreie
Eingabe vorausgesetzt). Deutlich sollte der Unterschied zur kanonischen
Normalform sein, da ich von vorn herein eine optimierte Variante meiner
Schaltung erhalte, was nicht ausschließt, dass weitere Möglichkeiten, dann
allerdings mit gleichem Aufwand existieren. |
|
|
|
|
|
|
Logische Schaltung erstellen |
Bauelemente-Auswahl |
Bauelementeauswahl-in Profilab testen |
Bauelemente-Auswahl optimieren |
|
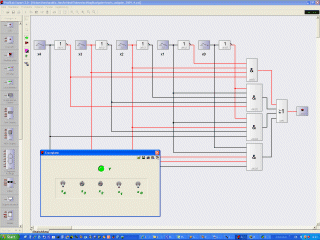
 ... und als
Profi-Lab 3.0-Schaltung |
wir benötigen:
- 3 × 5-Eingangs-OR
- 1 × 4-Eingangs-OR
- 1 × 4-Eingangs-AND
Problem: das gibt's aber so nicht - wir
entscheiden uns für folgende zwei Lösungen:
- Lösung 1 - Preis und Verfügbarkeit
sind nicht abgeglichen!!!)
- 1 Stück 3 × 3-Eingangs-NOR 7427
- 1 Stück 2 × 4-Eingangs-NAND (eingangsnegiert wird das zum "OR"
- 3 × 6-fach-Negaotor 7406
- Lösung 2 - wahrscheinlich das technische Optimum - da haben wir aber
noch nicht Preis und Verfügbarkeit abgeglichen!!!)
- 3 Stück 1 × 8-Eingangs-NAND 7430 (eingangsnegiert wird das zum "OR")
- 1 Stück 2 × 4-Eingangs-NAND 7420 oder alternativ 7440 (7440 ist
bezüglich seiner integrierten Treibereigenschaften besser)
- 1 × 6-fach-Negaotor 7406
|
... und als
Profi-Lab 3.0-Schaltung
Anmerkung:
die Schaltung ist erst einmal vollständig entwickelt - die verfügbaren
NAND's sind wieder auf AND transformiert und das benötigte OR wird aus einem
eingangsnegiertem AND generiert |
... und als
Profi-Lab 3.0-Schaltung
Anmerkung:
die Schaltung ist schon optimiert und aufeinanderfolgende Negatoren
herausgelöst |
|
elektrische Schaltung entwickeln |
Schaltung auf Expermentalplatine aufbauen |
Leiterplattenentwicklung |
Nutzung/Wartung |
|
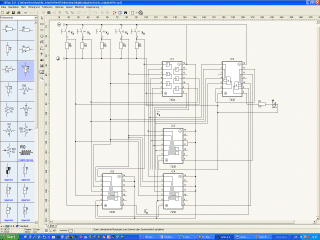
 ... und als
S-Plan-Schaltplan
Anmerkung:
die Schaltung ist entsprechend der Optimierungsvariante entwickelt |
das
"Elektronik-Projekt" |
|
|
|
... das ZIP-Archiv
komplett auspacken und die .EXE-Datei starten
Download
als CorelDraw11.0-Datei
