| 3.4. Aktive elektronische Bauelemente - Halbleiter |
|
|
Letztmalig dran rumgefummelt: 03.02.08 09:50:43 |
|
|
Vor mehr als 100 Jahren, 1874, veröffentlichte der deutsche Physiker K. F. Braun - bekannt geworden vor allem durch die Erfindung der nach ihm benannten „Braun'schen Elektronenstrahlröhre“ - eine Arbeit über Stromleitung von Sulfidkristallen. Er berichtete darin über seine Entdeckung, dass bestimmte Schwefelverbindungen bei Anlegen einer Spannung Strom in einer Richtung gut, in der anderen dagegen schlecht leiten. Viel Beachtung fand die Arbeit damals freilich nicht. Etwa drei Jahre später aber entsann man sich ihrer wieder, als nämlich die aufkommende Funktechnik einen Indikator zum Nachweis von Radiowellen erforderte. Das musste ein Bauelement mit gleichrichtender Wirkung sein. Brauns Sulfidkristalle mit aufgesetzter Metallspitze lieferten das in Form des „Kristalldetektors“. 1906 verwendete hierfür H. C. Dunwoody einen Karborundkristall zwischen Metallelektroden, G. W. Pickard schlug im gleichen Jahr schon einen Siliziumdetektor mit Spitzenkontakt als HF-Gleichrichter vor. | |||||||
|
1. Halbleitermodell und Leitungsvorgänge 2. Halbleiterdotierung - Gleichrichter 3. np- und pn-Übergänge 4. Stromfluss und Stromsperren 5. Verwandte Themen 6. Weblinks zum Thema 7. Hochinteressant: Halbleiterindustrie der DDR |
||||||||
|
| 1. Halbleitermodell und Leitungsvorgänge |
|
|
|
|
|
Eine in vielerlei Hinsicht dominierende Rolle nehmen die elektronischen
Halbleiter in der modernen Elektronik ein, zu denen insbesondere die Elemente Germanium und Silizium gehören.
Nicht auf den elektrischen Widerstand, wie man es der Bezeichnung entnehmen könnte, sondern auf den eigentümlichen Leitungsmechanismus kommt es hierbei an. Er ist physikalisch so interessant, dass wir ihm einige Aufmerksamkeit
widmen müssen. Notwendig sind jedoch einige Vorbemerkungen. Die Elemente Germanium und Silizium können als Halbleiter nicht so verwendet werden, wie sie aus ihren natürlichen Rohstoffen gewonnen werden und wie sie nach entsprechender Aufarbeitung im herkömmlichen Sinn als «chemisch rein» zu bezeichnen wären. Vorbedingung für das Zustandekommen der eigentlichen Halbleitereffekte ist eine so extreme Reinheit der Stoffe, wie sie weder in der freien Natur anzutreffen noch mit den in der Chemie üblichen Verfahren erreichbar ist. Wenn Germanium als Halbleiter brauchbar sein soll, darf auf eine Milliarde Germaniumatome nicht mehr als ein einziges Fremdatom entfallen. Das entspricht einem Reinheitsgrad von 99,999 999 9 %. Beim Silizium ist die Forderung noch tausendmal strenger. Was bedeutet demgegenüber schon die Reinheit besten Elektrolytkupfers von nur 99,99 %! |
||||||||||||||||||
|
|||||||||||||||||||
| Es werden also ganz ungewöhnliche technologische Bedingungen und Verfahrensweisen vorausgesetzt, die streng genommen nicht zur Physik im herkömmlichen Sinn gehören. Doch wir erkennen wieder, welch mächtige Impulse die
technischen Bedürfnisse und Erfindungen der Physik geben und wie ganze große Bereiche der Physik daraus entstehen. Physik und Technik schließen daher weder einander aus, noch stehen sie im Verhältnis einer Rangordnung. Vielmehr
stehen sie schon seit ihren ersten Anfängen in engster Wechselwirkung miteinander, und es wird immer wieder deutlich, «dass die viel gerühmte Einheit des Menschen mit der Natur in der Industrie von jeher bestanden und in jeder
Epoche ... anders bestanden hat» (Karl Marx). Die physikalischen Vorgänge in den Halbleitern sind leicht zu verstehen. Germanium und Silizium sind chemisch vierwertig wie der Kohlenstoff und kristallisieren in tetraedrischer
Grundanordnung (Bild unten). Bei der Temperatur des absoluten Nullpunktes sind alle Elektronen fest gebunden, so dass sich das Bild eines vollkommenen Isolators bietet. Das Bändermodell zeigt jedoch den wesentlichen Unterschied. Während der Bandabstand beim Isolator so groß ist, dass es keinem Elektron gelingt, ihn zu überspringen; ist hier der Abstand sehr schmal. Zwischen dem Valenzband, das mit den fest gebundenen Valenzelektronen voll besetzt ist, und dem nächsten, noch unbesetzten Band, dem Leitungsband, liegt ein Energiezwischenraum, der beim Germanium nur 0,75 eV und beim Silizium 1,2eV beträgt (Bild unten). Schon eine geringe Zufuhr an thermischer Energie genügt, um zahlreiche Elektronen in das Leitungsband zu heben, wo sie sich als Träger des elektrischen Stromes frei bewegen können. Gegenüber einem Metall sind es allerdings recht wenig, etwa 2,5 - 1033 Elektronen je Kubikzentimeter im Germanium bei Zimmertemperatur (bei Kupfer sind es 3,4 --1022 im gleichen Volumen!). Das hat einen recht hohen spezifischen Widerstand zur Folge und den Halbleitern auch ihren Namen eingebracht. Das Elektronengas ist deshalb auch nicht entartet und unterliegt der klassischen Statistik. Auch das Temperaturverhalten ist anders als bei den Metallen. Mit steigender Temperatur treten immer mehr Elektronen in das Leitungsband über, was eine ganz natürliche Folge der zunehmenden Auflockerung des Gittergefüges infolge der Wärmebewegung ist. Der spezifische Widerstand sinkt mit zunehmender Temperatur. Das ist der Zustand der Eigenleitung. Um die weiteren Einzelheiten des Vorgangs deutlicher vor Augen zu haben, ist es meist üblich, das im Bild unten dargestellte Kristallmodell zweidimensional zu schematisieren und in einer Ebene auszubreiten (Bild). Die rot hervorgehobenen Elektronen sind alle in Höhe des Leitungsbandes zu denken. Wir sehen jetzt, dass jedes der bei Erwärmung frei gewordenen Elektronen im Gittergefüge eine leere Stelle hinterlässt. Sie wird kurzerhand als Loch bezeichnet. Da das ungestörte Kristallgitter elektrisch neutral ist, bedeutet das Fehlen einer negativen Ladung an der Stelle des Loches soviel, als sei hier eine gleich große positive Ladung vorhanden. Daher rührt auch die oft verwendete Bezeichnung Defektelektron. Der reine Halbleiter enthält also im Zustand der Eigenleitung ebenso viele frei bewegliche negative Elektronen wie positive Löcher. Das mag wie ein bloßes Gedankenspiel anmuten. Aber die Löcher wirken physikalisch genauso, als säßen an ihrer Stelle positive Ladungen. Das zeigt sich sogleich, wenn man den Kristall mit einer Spannungsquelle verbindet. Die Löcher wandern zum Minuspol, die Elektronen zum Pluspol. Natürlich können sich die Löcher in Wirklichkeit nicht vom Fleck bewegen. Es kommt aber auf dasselbe heraus, wenn sich ein Elektron aus einer benachbarten Paarbindung löst und in ein Loch hineinspringt (Bild 79/4). An dieser Stelle ist das Loch jetzt verschwunden. Doch zuvor hat das Elektron bei seinem Sprung ein anderes, in Richtung des Minuspols gelegenes Lochhinterlassen. Das ursprüngliche Loch ist gewissermaßen näher an den Minuspol herangerückt. Die Anzahl der Elektronen und Löcher im Kristall bleibt auf diese Weise stets konstant. Es geht also ähnlich zu wie in einem schlecht besuchten Kino, in dem noch viele gute Plätze frei sind. Im Finstern, wenn es niemand sieht, rücken die Zuschauer einer nach dem andern nach hinten. Am Ende der Vorstellung sieht es dann so aus, als seien nur die leeren Stühle nach vorn gewandert. Vom physikalischen Standpunkt handelt es sich hier ebenfalls um einen «Strom von Löchern». |
|||||||||||||||||||
|
|||||||||||||||||||
|
|||||||||||||||||||
|
| 2. Halbleiter-Dotierung und deren technische Anwendung - Gleichrichter |
|
|
|
|
|
Dass die Halbleiter den Strom schlecht leiten, ist ein nur geringfügiger Nachteil, da die daraus hergestellten Bauelemente so klein oder dünnschichtig sind, das ihr Widerstand kaum eine Rolle spielt. Viel wichtiger sind die Möglichkeiten, die ein weiterer Kunstgriff der Halbleitertechnik eröffnet: Durch Zugabe, oder wie man auch sagt, durch Dotieren mit winzigen Mengen anderer Stoffe lässt sich der Charakter eines Halbleiters willkürlich weitgehend
verändern. Man kann es z. B. so machen, dass während der Herstellung des Materials eine genau berechnete Menge eines chemischen Elementes zugegeben wird, das der fünften Gruppe des Periodensystems angehört, z. B. Antimon (Sb). Dieses ist aber fünfwertig und hat demnach ein Valenzelektron mehr als das Germaniumatom. |
||||||||
| Trotzdem werden die Antimonatome in genau gleicher Weise in den Kristall eingebaut, das Wirtsgitter bleibt dabei unverändert (Bild
unten). Die Bindung der überzähligen Elektronen an die Fremdatome ist mit 0,5 eV sehr schwach, so dass die bei normaler Temperatur vorhandene thermische Energie des Gitters ausreicht, sie als Leitungselektronen in Freiheit zu setzen. Die Anzahl der ursprünglich vorhandenen Elektronen wird beträchtlich vergrößert. Das Ergebnis ist ein n-Leiter (Elektronen-Überschuss-Halbleiter). Bei näherem Zusehen geht das aber keineswegs so einfach vor sich, wie es nach außen hin den Anschein hat. Die bei höherer Temperatur vonstatten gehende Bildung von Elektronen und Löchern muss man sich vielmehr als einen Prozess vorstellen, der ebenso gut auch in umgekehrter Richtung vor sich gehen kann. Beim zufälligen Zusammentreffen eines Elektrons mit einem Loch verschwindet dieses Paar. Bei der Unregelmäßigkeit der Bewegung und der großen Anzahl der Teilchen wird sich das sogar sehr oft ereignen. Da jedoch bei konstanter Temperatur die Eigenschaften des Halbleiters trotzdem unverändert bleiben, muss die Zahl dieser Rekombinationen (Wiedervereinigungen) genau gleich der der neuen Paarbildungen sein. Oder auch anders ausgedrückt: Die Anzahl der Elektron-Loch-Paare nimmt nur so lange zu, bis dieser Vorgang durch den gegenläufigen Prozess der Rekombination kompensiert wird. Es bildet sich ein dynamisches Gleichgewicht heraus, im Grunde genommen ein Ergebnis des Zufalls, wie wir es in der Thermodynamik ausgiebig kennen gelernt haben. Überlegen wir noch, wieso der Rekombinationsvorgang zu diesem Gleichgewicht führen muss. Zwecks vergleichbarer Ergebnisse werden wir uns dabei immer auf Vorgänge in der Volumen- und Zeiteinheit beziehen. Offenkundig - und das ist die einfachste denkbare Möglichkeit ist die Anzahl der Rekombinationen proportional der Zahl der Elektronen, da ein jedes die gleiche Chance hat, per Zufall auf ein Loch zu treffen. Das aber hängt wiederum von der Anzahl der vorhandenen Löcher ab. Die Anzahl der Rekombinationen hängt sowohl von der Anzahl der Elektronen n als auch von der Anzahl der Löcher p ab, oder noch kürzer: sie ist dem Produkt n -p proportional. Die Bilder unten sollen das an einem ganz einfachen und extrem schematisierten Beispiel erläutern. Es seien anfangs in der Volumeneinheit 8 Elektronen und 8 Löcher vorhanden. Mit dem Proportionalitätsfaktor 1 finden damit in der Volumen- und Zeiteinheit 8 - 8 = 64 Rekombinationen statt. Da wir den Fall des Gleichgewichtes voraussetzen, werden sich in der gleichen Zeit auch 64 neue Paare bilden, womit der Zustand von Bild 80/2a im Zeitmittel erhalten bleibt. Jetzt wird der Halbleiter dotiert, und zwar mit Elektronen, wodurch die Anzahl der Elektronen sich verdoppeln möge. Das Produkt n' - p' muss konstant bleiben, d. h. nach wie vor gleich 64 sein, denn die Anzahl der Rekombinationen darf sich nicht ändern, weil die Anzahl der Paarbildungen ebenfalls konstant bleibt. Wenn aber der eine Faktor des Produktes n' = 16 ist, muss der andere auf p' = 4 zurückgehen (Bild 80/2b). Die Anzahl der Löcher wird durch die Zugabe von Elektronen demnach ganz beträchtlich zurückgedrängt. Chemikern ist dieses Verhalten übrigens durchaus geläufig. Sie bezeichnen es als Massenwirkungsgesetz. In seiner einfachsten Form lautet es: Im Gleichgewichtszustand ist das Produkt der Konzentrationen der je Zeiteinheit miteinander reagierenden Teilchenarten stets konstant. Bild 80/2c stellt schließlich den Zustand nach Dotieren mit einem Element aus der dritten Gruppe des Periodensystems dar. So kann sich beispielsweise ein Indiumatom völlig gleichwertig an die Stelle eines Germaniumatoms setzen. Da es aber anstatt 4 Valenzelektronen nur deren 3 mitbringt, fehlt an diesem Platz jetzt ein Elektron. Es entsteht ein zusätzliches Loch (Bild 80/3), aus dem reinen Halbleiter wird auf diese Weise ein p-Leiter (Elektronenmangel-Halbleiter). Alle unsere bisherigen Betrachtungen können sinngemäß auch auf diesen Fall angewandt werden. Am Ende folgt daraus, dass die Stromleitung fast ausschließlich von Löchern besorgt wird. Die Elektronen sind zu Minoritätsträgern degradiert. Dass es in Wirklichkeit wieder nur Elektronen sind, die, von einem Loch zum andern hüpfend, die Bewegung von Löchern nur vortäuschen, braucht nicht weiter zu stören. Es rechnet sich einfacher und macht weniger Umstände, wenn man sagt, es strömen nach dem Anschluss der Spannungsquelle positive Defektelektronen von Plus nach Minus. |
|||||||||
|
| 3. pn- und np-Übergänge |
|
|
|
|
|
n- und p-Leiter sind erst die Vorstufen zum Bau jener Halbleiterbauelemente, die für die elektronische Technik geradezu eine Wende bedeuteten. Neuartige Effekte wurden besonders durch Kombinieren mehrerer Leitertypen
erzielt. Auf welche Weise man n- und p-Leiter dabei verbindet, ist eine technische Frage. Sie lassen sich miteinander verschweißen oder zusammenlegieren, man kann den einen auf den anderen aufdampfen oder die Kombination
aus einem Stück herstellen, das abschnittsweise unterschiedlich dotiert wird. Wichtiger sind für uns die physikalischen Vorgänge an der Übergangsstelle, wo n-Leiter und p-Leiter aneinandergrenzen. Im Augenblick ihrer Berührung wandern Elektronen aus dem n-Leiter in den p-Leiter und Löcher aus dem p-Leiter in den n-Leiter hinein. Es ist ein Diffusionsvorgang wie bei zwei Gasen, deren Moleküle sich ganz von selbst vermischen (Bild unten). Bei unseren Halbleitern aber erreicht die Diffusion schnell einen bestimmten Endzustand und hört dann auf (Bild 81/2). Sie erstreckt sich auf eine dünne Übergangsschicht von wenigen tausendstel Millimeter Dicke und ist auf dem Bild übertrieben breit dargestellt. |
|
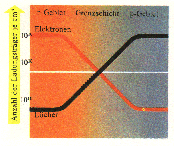
Um die Verhältnisse der Wirklichkeit mit einigen zahlenmäßigen Angaben zu belegen, können wir bei Zimmertemperatur im Zustand der Eigenleitung etwa 2,5 - 10'3 Elektronen und
Bild 81/3. Verlauf der Ladungsträgerkonzentration im n-p-Übergang ebenso viele Löcher je Kubikzentimeter annehmen. Das Produkt n - p ist dann 6,25 - 1028. Bei mäßiger Dotierung haben wir mit etwa 1018 Elektronen je Kubikzentimeter zu rechnen, was eine Verminderung der Löcher auf 6,25 - 1010 nach sich zieht (Massenwirkungsgesetz!). Ausgehend vom n-Gebiet, nimmt die Konzentration der Elektronen bis ins p-Gebiet hinein fast um den Faktor 108 ab. Das Umgekehrte gilt für die Konzentration der Löcher, die bei gleich starker Dotierung in der Gegenrichtung in gleichem Maße abnimmt. Der kontinuierliche Rückgang der Ladungsträgerkonzentration innerhalb der Grenzschicht ist im Bild 81/3 durch zwei Kurven dargestellt. In der Mitte, wo sich die Kurven schneiden, sind beide Arten von Ladungsträgern in gleicher Anzahl vorhanden. Da nach dem Massenwirkungsgesetz das Produkt ihrer Konzentrationen unverändert bleiben muss, dürfen hier nur je 2,5 - 10'3 Ladungsträger anwesend sein. Ihre absolute Anzahl ist daher 200mal geringer als zu beiden Seiten des Übergangs; denn die Summe beträgt hier nur 5 - 10'3 je Kubikzentimeter gegenüber 1018. Der n-p-Übergang ist daher an Ladungsträgern verarmt. Der Grund für die begrenzte Wirkung der Diffusion liegt darin, dass es sich eben nicht um neutrale Gasmoleküle, sondern um elektrisch geladene Teilchen handelt. Die ins p-Gebiet übergewechselten Elektronen hinterlassen im n-Gebiet positiv geladene Ionen, d. h. Atomrümpfe, denen sie ursprünglich einmal angehörten. Die ins n-Gebiet eingewanderten Löcher hinterlassen eine entsprechende negative Raumladung im p-Gebiet. Dazwischen spannt sich ein elektrisches Feld aus, dessen Plus-Minus-Richtung vom n-Gebiet nach dem p-Gebiet weist. Je mehr Ladungsträger herüber und hinüber diffundieren, desto stärker wird das von den zurückbleibenden ortsfesten Ionen gebildete Feld. Schließlich hört die Diffusion auf. Dass sich hier kein ruhender Zustand ausbildet, sondern wiederum ein dynamisches Gleichgewicht vorliegt, wollen wir jetzt nicht weiter beachten. Die eigentümliche Wirkung der Grenzschicht macht sich nun geltend, wenn eine elektrische Spannung an die Kombination gelegt wird. Es gibt zwei Möglichkeiten. Im ersten Fall sei der Minuspol an die n-Seite und der Pluspol an die p-Seite gelegt (Bild 81/4a). Das von der Spannungsquelle herrührende Feld ist somit demjenigen in der Grenzschicht entgegengerichtet und hebt es auf. Die zum Stillstand gekommene Diffusion kann jetzt ungehemmt weitergehen. Elektronen und Löcher strömen in Scharen auf die andere Seite. Es fließt ein Strom, der nur durch den Widerstand des Materials begrenzt wird. Man spricht dabei von der Polung in Fluss- oder Durchlassrichtung. Anders ist es, wenn der Pluspol an die n-Seite und der Minuspol an die p-Seite angeschlossen werden (Bild 81/4b). Das äußere Feld hat jetzt dieselbe Richtung wie das Feld in der Grenzschicht, das somit verstärkt wird. Es unterbindet den Übergang von Elektronen und Löchern auf die Gegenseite noch mehr als vorher. Man könnte auch sagen, dass in diesem Fall Elektronen und Löcher nach beiden Seiten hin aus der Grenzschicht herausgezogen werden. Die Grenzschicht verbreitert sich und stellt einen sehr großen Widerstand dar. Auf jeden Fall kann bis auf einen kümmerlichen Rest, den sogenannten Sperrstrom*, jetzt kein Strom fließen. Die Kombination ist in Sperr-Richtung gepolt. Die n-p-Kombination wirkt jetzt wie ein Ventil, das nur eine Stromrichtung zulässt. Der geringfügige Sperrstrom spielt praktisch keine Rolle. Das Verhältnis der Ströme in den beiden Richtungen kann bis zu 1011:1 betragen. Die n-p-Kombination ist deshalb ein vorzüglicher Gleichrichter für Wechselströme aller Art. Aus der Technik ist sie nicht mehr wegzudenken. Von den winzig kleinen Halbleiterdioden (Bild 81/5) in zahlreichen elektronischen Geräten bis zum Hochleistungs-Siliziumgleichrichter der Starkstromtechnik für Sperrspannungen bis 800V und Ströme bis 1000 A ist sie jedem Elektrotechniker wohlbekannt. |
|
|
|
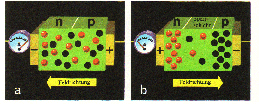
n-p-Kombination mit angelegter Spannung |
| 4. Stromfluss und Stromsperren |
|
|
|
|
|
Man spricht von einer Ventilwirkung der Bauelemente in Bezug auf die Stromrichtung. Der Stromfluss ist nicht mehr in beiden Richtungen möglich. Dies bewirken grundsätzlich Dioden. |
| 5. Verwandte Themen |
|
|
|
|
|
Die gesamte Palette der Halbleiterbauelemente muss nun hier als Verwandtschaft 1. Grades eingetragen werden. Irgendwie haben alle damit zu tun, wenngleich das Silizium gegenwärtig an Bedeutung verliert. Dabei muss man sehen, dass der Bedarf immer noch wachsend ist und sich das Silizium neue Anwendungen erschlossen hat. Insgesamt jedoch sind für die gegenwärtigen Frequenzen im GHz-Bereich auch andere Materialien non Nöten. | ||||
|
| 6. Weblinks zum Thema |
|
|
|
| 7. Hochinteressant: Halbleiterindustrie in der DDR |
|
|
|
|
Der Begriff „Mikroelektronik" ist kein Modewort, aber auch
kein Zauberwort, wenn manche Journalisten auch von der Wunderwelt der
„Winzlinge" berichten. Die Mikroelektronik ist die größte technologische
Herausforderung der Gegenwart. Und sie ist die entscheidende
Schlüsseltechnologie der wissenschaftlich-technischen Revolution, denn
Robotertechnik und Informatik; ja selbst Biotechnologie, sind ohne
Mikroelektronik als Grundlage nicht realisierbar. Wie begann es in der DDR? Die Entwicklung der Halbleiterproduktion in der DDR begann
1952 im Werk für Bauelemente der Nachrichtentechnik „Carl von Ossietzky" in
Teltow bei Berlin (später Stammbetrieb im VEB Kombinat Elektronische
Bauelemente). Eine Arbeitsgruppe unter Leitung von Prof. Dr. Mathias Falter
begann mit der labormäßigen Herstellung von Germanium-Spitzentransistoren. Diese
Transistoren hatten drei Steckerstifte, und wie bei Elektronenröhren erforderten
sie eine 3-polige Steckfassung für den Schaltungsaufbau: Das Halbleitermaterial
war n-leitendes Germanium. Im Abstand von 20 μm
waren zwei geätzte Spitzen (Emitter/Kollektor) aus Phosphorbronze aufgesetzt, in
deren Umgebung p-leitende Zonen durch Formieren erzeugt wurden. Damit entstand
die für den Transistor erforderliche Zonenfolge p-n-p. Bedeutsame Tagung des ZK der SED Von ausschlaggebender Bedeutung für die beschleunigte Entwicklung der Schlüsseltechnologie Mikroelektronik in der DDR war die 6. Tagung des Zentralkomitees der SED (23./24. 6. 1977), die die Durchführung der Beschlüsse des IX. Parteitages der SED auf dem Gebiet der Elektrotechnik und Elektronik zum Inhalt hatte. Der Beschluss dieser 6. Tagung des ZK der SED orientierte auf so wichtige Aufgabenstellungen wie
Wenn man damals, im Jahr 1986, Begriffe wie Mikroelektronik, Robotertechnik, flexible Fertigungsautomatisierung, Personalcomputer, CAD/CAM-Technik und andere im täglichen Sprachgebrauch verwendete, so war dies das Ergebnis einer erfolgreichen Politik bei der Durchsetzung des wissenschaftlich-technischen Fortschritts in unserem Land. Wie in allen führenden Industrieländern der Welt ist auch bei uns die Mikroelektronik mit ihrem schnellen Entwicklungstempo zur wichtigsten Basisinnovation geworden. Sie nimmt daher zu Recht in unserer Wirtschaftsstrategie eine Schlüsselstellung ein bei der Verbindung der wissenschaftlich-technischen Revolution mit den Vorzügen des Sozialismus. |
|
zur Hauptseite |
© Samuel-von-Pufendorf-Gymnasium Flöha | © Frank Rost Januar 2006 |
|
... dieser Text wurde nach den Regeln irgendeiner Rechtschreibreform verfasst - ich hab' irgendwann einmal beschlossen, an diesem Zirkus nicht mehr teilzunehmen ;-) „Dieses Land braucht eine Steuerreform, dieses Land braucht eine Rentenreform - wir schreiben Schiffahrt mit drei „f“!“ Diddi Hallervorden, dt. Komiker und Kabarettist |