Logikschaltungen - als Normalform sowie zusammengefasst

Meine Aufgabe bestand darin, aus der folgenden Wahrheitstabelle zwei Schaltpläne zu entwickeln. Zum einen in der kanonischen Normalform und zum anderen diese Normalform mit Hilfe eines KV-Diagramms zu vereinfachen.

Logiktabelle

 Diese Wahrheitstabelle hat 4 Ein- und 2 Ausgänge. Für jeden Ausgang soll eine separate LED leuchten. Am Ende muss für y₁ genau 5 mal eine LED leuchten und für y₀ genau 5 mal die LED nicht leuchten

kanonische Normalform

Um eine Logikschaltung aufbauen zu können muss man zunächst alle Werte für y₁ = 1 und y₀ = 0 herausschreiben. Für y₀ nimmt man die Werte die 0 sind, weil es da weniger gibt. Es gibt konjunktive sowie disjunktive Normalformen für binäre Signale (mehr geht, wird aber unendlich viel komplexer!). Diese formuliert man mit Hilfe von logischen Symbolen:

Somit ergibt sich: 

 

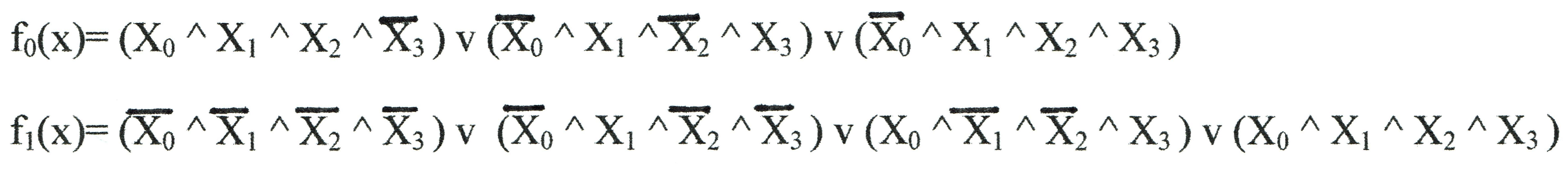
für y₀ = 1 = (x₀∧x₁∧x₂∧¬x₃)∨(¬x₀∧x₁∧¬x₂∧x₃)∨(¬x₀∧¬x₁∧x₂∧x₃)

für y₁ = 1 = (¬x₀∧¬x₁∧¬x₂∧¬x₃)∨(¬x₀∧x₁∧¬x₂∧¬x₃)∨(x₀∧¬x₁∧¬x₂∧x₃)∨(x₀∧x₁∧x₂∧x₃)

... in ProfiLab als Logik-Schaltplan umsetzen

Man braucht für die Schaltung 4 Eingänge und deren invertierte Werte, dann erstellt man fünf Vier-Eingangs Und-Bausteine, die sich alle mit einem Fünf-Eingangs Oder verbinden, der schließlich an eine LED angeschlossen ist (kanonisch disjunktive Normalform). Als nächsten braucht man sich nur noch von den Eingängen den Wert oder den negierten Wert "abzuholen" und mit dem entsprechenden Und-Baustein verknüpfen. Um y₀ zu realisieren, verwenden wir die kanonisch konjunktive Normalform. Hierfür tauschen wir einfach UND und-Oder-Bausteine aus und negieren die Eingänge. Das heißt wir nehmen unsere Formel zur Hand und negieren jede Variable, dann verbinden wir die negierten Eingänge mit den Oderbausteinen und schließlich mit dem Und-Baustein und der LED-Leuchte.

Karnaugh-Veitch Diagramm zur Schaltungsvereinfachung

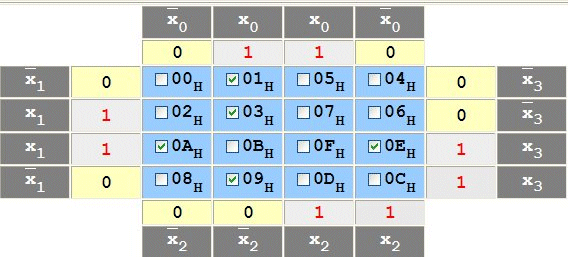
Mithilfe des Karnaugh-Veitch Diagramm werden nun die oben entstandenen Formeln für y₁ und y₀ vereinfacht. Dazu trägt man die Zahlen in die Tabelle ein - wie das funktioniert, erfährt man hier: Karnaugh-Tafeln

y1	UND	y0

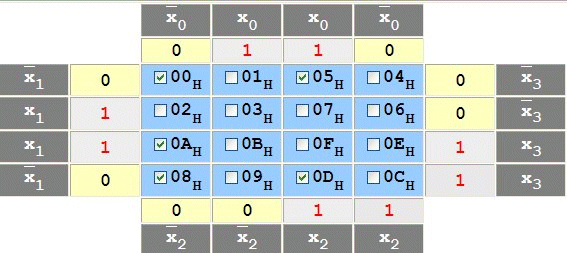Anschließend muss man die eingetragenen Felder zusammenfassen um die Vereinfachung zu bekommen. Dabei sind folgende Regeln zu beachten:

• wenn benachbarte Felder eine 1 enthalten, werden sie zusammengefasst
• diese Zusammenfassung darf keine Nullen enthalten
• die Zusammenfassungen müssen Rechtecke sein
• die Gruppen dürfen sich überlappen
• eine Gruppe darf nicht vollständig von einer anderen Gruppe umschlossen werden
• die Anzahl der Felder die man zusammenfasst, muss einer Potenz der Zahl 2 entsprechen, also 2, 4, 8, 16, ...
• die Zusammenfassung kann auch über die Ränder des Diagramms hinausgehen, alos z.B. Feld 3 und 7, oder 6 und 14

Damit ergibt sich für meine Werte: 

für y₁=1 = (x0∧¬x2∧¬x3)∨(¬x0∧x1∧x3)∨(x0∧¬x1∧¬x2∧x3) 

für y₀=0 muss man den Wert noch negieren daraus ergibt sich: (x0∧x1∧x2∧x3)∨(¬x0∧x1∧¬x2)∨(x0∧x2∧¬x3)

in SPlan umsetzen

Wenn man die Wahrheitstabelle mit ProfiLab dargestellt hat und alles soweit funktioniert, kommt der nächste Schritt und man Zeichnet einen Schaltplan. Dazu hab ich hier das Programm SPlan50 verwendet. Damit kann man den gesamten Aufbau der späteren Schaltung zeichen und sich schon einmal theoretisch überlegen wie alles angeschlossen werden muss. Dabei können schon für die AND, NAND, OR und NOR Bauteile die richtigen Positionen angeschlossen werden, sodass es später kein Problem mehr ist die Schaltung in der Praxis aufzubauen.

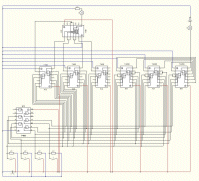
Normalisierte Schaltung dargestellt mit SPlan

Vereinfachte Schaltung dargestellt mit SPlan

Schaltung aufbauen

Wenn man anschließend den Schaltplan in der Praxis zu einer Schaltung zusammengefügt hat könnte das so aussehen: