| Das Teilerproblem |
|
|
Letztmalig dran rumgefummelt: 26.06.23 04:21:09 |
|
|
Die Baronin von Birlinghoven hat ihren beiden
Töchtern eine Truhe voller Goldmünzen hinterlassen. Ihr Testament bestimmt,
dass das Gold einem benachbarten Kloster zukommt, falls es den Töchtern
nicht gelingt, den Inhalt der Truhe wertmäßig genau in zwei Hälften
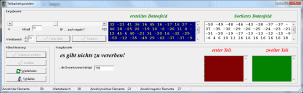
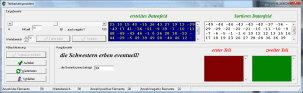
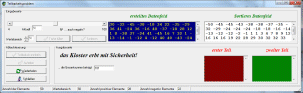
untereinander aufzuteilen. Die Goldmünzen haben nur ganzzahlige Werte. Beispiel: Eine Truhe Goldmünzen mit den Werten 1, 9, 5, 3, 8 Taler könnten die Töchter in die Hälften 1, 9,3 Taler und 5, 8 Taler teilen. Eine Truhe mit den Werten 1, 9, 7, 3, 8 Taler fiele an das Kloster, weil die Aufteilung nicht möglich ist. Aufgabe: Schreibe ein Programm, das bei Eingabe einer Folge ganzer Zahlen für die in der Truhe vorkommenden Werte die beiden Erbteile genau aufzählt, andernfalls das Erbe dem Kloster zuspricht, wenn eine Aufteilung nicht möglich ist. Erstelle mindestens fünf Beispiele mit verschiedenen Truheninhalten. Der Inhalt einer Truhe sei 15, 27, 39, 7, 23,56,13, 39, 22, 5, 42, 34 Taler. |
||||
|
1. Problembeschreibung 2. Hintergründe und Zusammenhänge - Einordnung in Klassen 3. Lösungsalgorithmen 4. Programmvorschläge 5. Zusammenfassung 6. Weiterführende Literatur 7. Linkliste zum Thema 8. Verwandte Themen |
|||||
|
|||||
| Quellen: LOG IN - Heft 146/147 (2007) Seite 47 ff. |
| 1. Problembeschreibung |
|
|
|
| Gegeben sei eine endliche Mengen ganzer Zahlen im Bereich von - ∞ bis + ∞, wobei die Frage lautet, ob sich die Gasamtmenge in jeweils wertmäßig gleiche Teile zerlegen lässt, wobei die gegebenen Zahlen immer den jeweiligen Teilen zugeordnet werden müssen? | |
Für kleine Mengen M ist das Problem empirisch durch ausprobieren möglich
- Beispiel:
|
|
| 2. Hintergründe, Zusammenhänge - Einordnung in Klassen |
|
|
|
|
|
Für kleine Mengen M ist das Problem empirisch durch ausprobieren möglich! Für große Mengen existieren allerdings keine anderen Verfahren, als genau diese: ausprobieren jeden Elements mit jedem - das sind dann aber schon bei 10 Elementen 210 Möglichkeiten. |
| 3. Lösungsalgorithmus |
|
|
|
|
|
Die ersten Schritte sind hier vergleichsweise einfach und deren Lösung ordnet sich in die Menge der Anfänger-Aufgaben. Dies zumindest dann, wenn die zu teilende Gesamtmeng klein ist. |
| 4. Programmvorschläge |
|
|
|
|
|
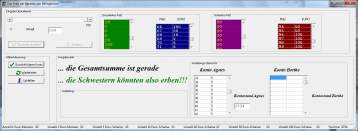
Das Gesamtproblem wurde schon einmal in seine Teilprobleme zwerlegt und diese, da sie aufeiender aufbauen, auch bereits programmtechnisch in solchen Stufen umgesetzt. Schritt ein war hierzu das Erfassen der Grunddaten - also das Kreiieren einer Menge von ganzen Zahlen oder pseudorealen Geldwerten (im Beispiel in Euro). | ||||||
|
|||||||
|
|||||||
| 5. Zusammenfassung |
|
|
|
|
|
|
| 6. Weiterführende Literatur |
|
|
|
|
|
|
| 7. Links zum Thema |
|
|
|
|
|
|
| http://www.mathematische-basteleien.de/kaprekarzahl.htm | |
| 8. Verwandte Themen |
|
|
|
|
|
Das Vorangestellte hilft wirtschaften, löst jedoch kein einziges Problem (allerdings ohne Beachtung der Worst-Case-Strategien wird man auch nicht erfolgreich Software entwickeln und/oder informatische Projekte realisieren können). Deshalb nunmehr das, was wirklich Arbeiten hilft. | ||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
|
|
|
zur Hauptseite |
© Samuel-von-Pufendorf-Gymnasium Flöha | © Frank Rost am 24. Dezember 2007 |
|
... dieser Text wurde nach den Regeln irgendeiner Rechtschreibreform verfasst - ich hab' irgendwann einmal beschlossen, an diesem Zirkus nicht mehr teilzunehmen ;-) „Dieses Land braucht eine Steuerreform, dieses Land braucht eine Rentenreform - wir schreiben Schiffahrt mit drei „f“!“ Diddi Hallervorden, dt. Komiker und Kabarettist |
|
Diese Seite wurde ohne Zusatz irgendwelcher Konversationsstoffe erstellt ;-) |