Projekt Kombinatorik am Gymnasium Flöha 2006

Projekt Logik & Kombinatorik am Gymnasium Flöha im Schuljahr 2006 - The Making Of

Letztmalig dran rumgefummelt: 21.12.17 18:59:12

leicht erkennbar - das Prinzip: vom Einfachen zum Schwierigen
logische Aussagetechniken und deren verzwickte Lösungen kennen zu lernen - das fängt ganz einfach schon mit den Begriffen "wahr" und "falsch" an und setzt sich fort in den logischen Grundaussagen "und", "oder" sowie "nicht"
schon haben wir eigentlich komplette Verwirrung gestiftet, denn nunmehr kann man das alles miteinander kombinieren - schwupp, schon ist das alles andere als einfach
an alles hängen wir dann noch die Mikroelektronik an und brauchen durchaus für das Gruppenprojekt das Semester über Zeit, um zu sinnvollen Lösungen zu kommen
der Clou: das alles ist auf Software abzubilden - na dann 'Prost Mahlzeit!" ;-)
PS: der Kurs hat sich in der Veranstaltung der TU-Freiberg zur Bool'schen Algebra wacker geschlagen, denn so ganz unbeleckt war man insgesamt nicht, wobei das Thema jeden von der Straße gegriffenen "Normalverbraucher" nach dem dritten Satz allein gelassen hätte ;-)

Das offizielle Logo ...

... und das inoffizielle Logo ;-)

Projekt Logik & Kombinatorik

1. Projektidee
2. Arbeitsgruppen und Verweise
3. Die Arbeiten am Projekt
4. Die Ergebnispräsentationen
5. Verwandte Projekte

1. Grundidee des Projektes

Entscheidender Impuls war, wie schon so oft, eine Problemklasse in die Arbeitsgruppen zu bringen, die so vorher bei uns noch nicht gelöst worden ist. Und vor allem: auch Programmierprofis müssen noch ein Betätigungsfeld vorfinden, auf welchem sie sich wie alle anderen bewähren müssen. Entscheidend für die Informatikprojekte ist aber auch der Ansatz, keine Projekte für den Mülleimer zu produzieren. Wir schaffen uns kleine Werkzeuge, welche später einmal das Leben leichter machen sollen.

mit den Kombinationen von UND, ODER sowie NICHT lassen sich logische Kombinationen herstellen, welche auch noch ineinander geschachtelt sein können

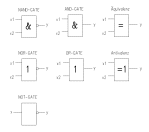
Logische Grundschaltungen

Eine Hauptaufgabe der mathematischen Logik ist die Untersuchung des formalen Denkens und Schließens mit Hilfe mathematischer Methoden, die z. B. der Algebra und der Algorithmentheorie entnommen sind.
Diese ursprünglich aus der Philosophie stammende Aufgabe ist jedoch nicht ihre einzige; die mathematische Logik umfasst heute eine Vielzahl von Fragestellungen und Anwendungen auf den verschiedensten Gebieten, z. B. in den Naturwissenschaften, in der Schaltalgebra, in der Theorie informationsverarbeitender Systeme, in der Linguistik und in verschiedenen Disziplinen der Gesellschaftswissenschaften wie Philosophie, Rechtswissenschaft und Ethik.

Bool'sches Aussagenkalkül

aus einer Menge von Eingangsgrößen lassen sich nach bestimmten Formeln die Menge aller möglichen Kombinationen berechnen - bei 1 Eingang sind das 2 Kombinationen, bei 2 Eingängen sind das 4, bei 3 Eingängen sind das 8 usw. (dies gilt zumindest dann, wenn die Ein- aber auch Ausgangsgrößen binär sind - das heißt, zwei zustände aufweisen können

Kanonische Normalformen

auf diese möglichen Kombinationen lassen sich nun Bedingungen legen, welche einzelne Fälle einfach ausschließen - gesucht werden immer nur die Fälle, welche auf die gesetzten Bedingungen hin ein logisches "wahr" ergeben

es existieren nun eine ganze Reihe zwischenzeitlich recht erprobter Verfahren, um hier zu Lösungen zu gelangen (kanonisch konjunktive bzw. disjunktive Normalform) - diese liefern jedoch in fast jedem Falle die zwar immer funktionierende, jedoch auch umständlichste Lösung

dumm ist, dass solche Lösungen letztendlich in elektronische Schaltungen gepasst werden müssen - jeder Computer ist einen solche - zweckmäßig also, wenn man sie verkürzen könnte

Logik und Kombinatorik

diese ist möglich - ein Herr de Morgan hat dazu die entsprechenden Regeln geschaffen - diese sind übrigens auch aus der Mathematik bekannt (Assoziativgesetz, Distributivgesetz usw.) - sie heißen sogar genau so, werden aber eben nur auf Logikebene angewandt

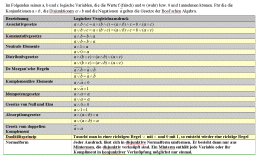
Logische Schaltungszusammenfassung

man kann natürlich auch zu sehr neuen Verfahren greifen - genannt seinen an dieser Stelle Karnaugh-Tafeln oder McCluskey-Verfahren - diese sind mathematisch anspruchsvoller, benötigen dafür jedoch keine Vereinfachung mehr sie vereinfachen selbst schon - im Falle von McCluskey sogar perfekt - da bekomme ich die kürzeste Form sofort, bzw. für den Fall, dass mehrere Lösungen existieren, eine davon

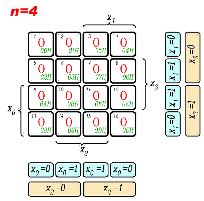
Karnaugh-Veitch-Tafeln

wenn man sich's finanziell für nicht ganz so große Logiken, jedoch enorme Stückzahlen 8so oberhalb 10 000 Produkte) leisten kann, so genannte "Programmable Logic Arrays"

logische Arrays

werden logische Aufgaben extrem unhandlich, so macht man sich gar nicht mehr die mühe, sie logisch analysieren, sondern verwendet ein so genannte EPROM-Logik

EPROM-Logik

Zum Schluss benötigt man den Vereis auf die Grundbauelemente der Digitalelektronik, wobei logisch die freie Wahl steht, TTL- oder CMOS-Logik zu verwenden - wir haben die 74-er TTL-Reihe eingesetzt

TTL-Liste

hier nun findet man die Fülle des theoretischen Hintergrundes zum gesamten Projekt - ist aber nur was für Hardcore-Logiker ;-)

Bool'sche Algebra

2. Arbeitsgruppen und Verweise

Auf der Grundlage der Kenntnisse zur Bool'schen Algebra sowie der Erstellung von Schaltnetzen, ihrer Zusammenfassung nach den de Morgan'schen Regeln oder Karnough-Tafeln soll nunmehr versucht werden, diesen gesamten Part einem Programm zu übergeben. In insgesamt 5 Projektteams musste unter Einsatz von Schweiß sowie Einbringung von Teamgeist Programmierarbeit mit einer bekannten Programmieroberfläche richtig professionell programmiert werden. Genaue Abstimmung ist für den Erfolg extrem entscheidend. Ein Projekt nahm dabei von vorn herein eine Sonderstellung ein - das Projekt EPROM-Logik.

Projekt EPROM-Logik:

Theorie Idee sowie Umsetzung Praxis

ein EPROM ist eine programmierbare Matrix (eingangsseitig als so etwas wie eine Schalttabelle, deren Ausgänge (0 oder1) festgelegt werden können - also genau das, was der Logikentwickler benötigt

jede logische Kombination von Eingängen A₀ bis A_n (typabhängig - größere Anzahl der Adresseingänge sollte 0 gesetzt bleiben) erhält eine Anzahl von Ausgangswerten - die Datenbits - in der Zählung ebenfalls immer von D₀ bis D₈)

Projekt Kanonisch Konjunktive Normalform:

Theorie Idee sowie Umsetzung Praxis

ein EPROM ist eine programmierbare Matrix (eingangsseitig als so etwas wie eine Schalttabelle, deren Ausgänge (0 oder1) festgelegt werden können - also genau das, was der Logikentwickler benötigt

jede logische Kombination von Eingängen A₀ bis A_n (typabhängig - größere Anzahl der Adresseingänge sollte 0 gesetzt bleiben) erhält eine Anzahl von Ausgangswerten - die Datenbits - in der Zählung ebenfalls immer von D₀ bis D₈)

Projekt Kanonisch Disjunktive Normalform:

Theorie Idee sowie Umsetzung Praxis

eine Logiktabelle mit maximal 5 Eingängen wird abgeleitet - die Ausgangswerte y werden vom Nutzer eingetragen

liegen mehrere Ausgänge vor, so muss die gesamte Schaltungsentwicklung so viele male durchlaufen werden, wie Ausgänge nutzerseitig definiert wurden

Frank Knietsch als Teamleiter und Organisator

Projekt Karnaugh-Veitch-Diagramme:

Theorie Idee sowie Umsetzung Praxis

eine vorgegebene Logiktabelle soll in eine möglichst kurzes Schaltnetz überführt werden

im Idealfall sind Anzahl der benötigten Eingänge sowie der Aufwand an einzusetzenden logischen Schaltfunktionen minimal

realisiert wird dies ausschließlich via Karnaugh-Tafeln

Projekt Lösung Logischer Probleme:

Theorie Idee sowie Umsetzung Praxis

ein viele Rätselzeitschriften machen es uns vor: wie verwirre ich den Rätsellöser mit scheinbar harmlos aussehenden Fakten und Bedingungen

Chancen zur Lösung hat nur ein systematisches Vorgehen - nämlich das Auffinden aller grundsätzlichen Möglichkeiten (Fakten) sowie das Anwenden der gegebenen Bedingungen auf diese

schwer tun sich einige mit der Lösung, dass es keine gibt - dabei können die Bedingungen so gegeneinander verriegelt sein, dass niemals eine wahre Gesamtaussage existiert

3. Die Arbeit am Projekt

	Basis für die Projektbearbeitung ist die Kenntnis der Grundgesetze der Logischen Algebra - heißt zu gut deutsch nichts anderes, als finde in kürzester Form wahre Aussagen. Dass man zu diesem Ergebnis mit durchaus verschiedenen logischen Ansätzen gelangen kann, zeigen nun unsere Projekte
	in jedem Falle, in welchem es um Logikschaltungen ging, muss erst einmal in irgend einer Art und Weise die Schaltfunktionstabelle generiert werden (bei den Karnaugh-Veitch-Tafeln wurde der Aufwand sinnvoll reduziert und die Eingangsanzahl mit 5 begrenzt)
	diese ist abhängig von der Anzahl der Eingänge x₀ bis x_n sowie der Anzahl der Ausgänge y₀ bis y_n
	die Anzahl der möglichen logischen Kombinatinen für Binärsysteme ergibt sich aus: anzahl_kombinationen =2 ^{anzahl_eingaenge}
	mit diesen Eingangsdaten kann das Programm mit sich selbst in Klausur gehen und ein Schaltwerk entwickeln (das ist eine logische Funktion, welche genau die gesetzten Eingangsbedingungen korrekt und immer erfüllt)
	diese ist zwar in jedem Falle korrekt, oft aber zu lang - die de Morgan'schen Theoreme helfen zu kürzen
	Schlussendlich muss der Schaltplan entwickelt werden

4. Die Ergebnis-Präsentation des Projektes

5. Verwandte Projekte

zur Hauptseite

... dieser Text wurde nach den Regeln irgendeiner Rechtschreibreform verfasst - ich hab' irgendwann einmal beschlossen, an diesem Zirkus nicht mehr teilzunehmen ;-)

„Dieses Land braucht eine Steuerreform, dieses Land braucht eine Rentenreform - wir schreiben Schiffahrt mit drei „f“!“

Diddi Hallervorden, dt. Komiker und Kabarettist

Diese Seite wurde ohne Zusatz irgendwelcher Konversationsstoffe erstellt ;-)