Beispiele:
nicht gegen die Fano-Bedingung verstoßen:
gegen die Fano-Bedingung verstoßen:
- Morse-Code (der Code für E ist auch Anfang vieler anderer
Codes wie A, F, H, I, J usw)
- die deutsche Sprache / bzw. Sprachen allgemein (z.B. ist "bei" auch
in "Beispiel" enthalten)
Wie kann man aber mit 2 Zuständen Dinge komprimieren?
Als 2 Zustände wähle ich die binären Zustände 0 und 1. Man kann z.B.
definieren, dass ein Code immer auf 0 enden muss. So ist klar, wann der
nächste Buchstabe beginnt. Muss man nur wenige verschiedene Zeichenketten
codieren, bietet sich ein Baum an, bei dem man definiert: 0 ist eine Verzweigung
nach links und eine 1 ist eine Verzweigung nach rechts. Für die Buchstaben
A bis E ergibt das:
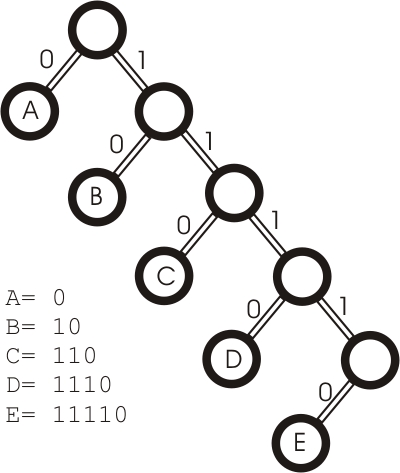
Wie man sicherlich schon erkennen kann ist dieses Verfahren bei weitem
nicht optimal, so ergeben sich bereits bei 10 verschiedenen Zeichen unnötig
lange Codes.
Mit dem Thema der optimalen Bäume beschäftigte sich lange Jahre David
Huffman und hat ihn gefunden.


 Alle
Mandelbrot-Grafiken bereitgestellt von André Neubert Klassenstufe
12,
Alle
Mandelbrot-Grafiken bereitgestellt von André Neubert Klassenstufe
12,