 |
Grundlage des RSA-Verfahrens
sind mathematische Einwegfunktionen. In der einen Richtung müssen sie ganz
einfach lösbar, in der anderen theoretisch nicht mehr in sinnvoller Zeit
realisierbar.
Den Namen hat das Verfahren von Ronald Rivest, Adi Shamir
und Leonard Adleman, den drei Männern, die es 1977 erfunden
haben. RSA ist ein asymmetrisches Verfahren, es gibt also einen public key
und einen private key. Beide werden über Primzahlen gebildet. Außerdem geht
in das Verfahren die Modulo-Rechnung ein.
Die grundsätzliche Idee lautet: verschlüsseln kann jeder - entschlüsseln
lediglich authorisierte Personen (das sind diejenigen, welche den geheimen
Schlüssel besitzen) |
 |
Vor- und Nachteile des Verfahrens
- es muss kein Schlüssel ausgetauscht werden
- der Schlüssel ist sehr sicher
- es handelt sich in der Grundversion jedoch um
eine monoalphabetische Substitutions-Chiffre
- dieser ist in sich so anfällig, wie ein
CÄSAR-Chiffre
- zum Knacken des Chiffre benötige ich gar keinen
Chiffre - das erledigt eine relativ einfache Häufigkeitsanalyse
|
 |
Wie funktioniert der RSA-Verschlüsselungsalgorithmus? Die
Caesarverschiebung ist das klassische Beispiel eines konventionellen, so
genannten symmetrischen Verschlüsselungsalgorithmus: Sowohl dem Sender als
auch dem Empfänger der geheimen Nachricht ist der Schlüssel e bekannt (und
damit auch der zweite Schlüssel d, der sich leicht aus e berechnen lässt).
Das bedeutet aber, dass der geheime Schlüssel e zwischen Sender und
Empfänger zunächst ausgetauscht werden muss, bevor verschlüsselt werden
kann. Steht nun für diesen Austausch kein sicherer Weg zur Verfügung,
sondern nur ein öffentliches Medium wie z. B. das Internet, dann wird eine
sichere Schlüsselvereinbarung zwischen Sender und Empfänger ein Problem.
Eine Alternative bieten so genannte asymmetrische oder Public Key
Verschlüsselungsverfahren. Hier besitzt jeder Teilnehmer zwei Schlüssel:
einen privaten Schlüssel (private key), den er geheim hält, und einen
öffentlichen Schlüssel (public key), der aller Welt bekannt gegeben wird
(wie eine Telefonnummer in einem Telefonbuch).
Wenn Sie mir nun eine geheime Nachricht senden möchten, schlagen Sie einfach
im entsprechenden öffentlichen Verzeichnis meinen öffentlichen Schlüssel
e (encrypt
engl. verschlüsseln) nach, verschlüsseln damit die Nachricht und senden sie
dann als Email an mich. Da nur ich den zugehörigen geheimen Schlüssel d (decrypt
i engl. entschlüsseln) kenne, bin nur ich in der Lage, dieses Email wieder
zu entschlüsseln.
Nun liegt es aber in der Natur der Sache, dass der Zusammenhang zwischen der
originalen und der verschlüsselten Nachricht eindeutig sein muss, und daraus
kann man ableiten, dass auch der geheime Schlüssel d prinzipiell aus (lern
öffentlichen Schlüssel e berechenbar sein muss. Es scheint also, dass es ein
solches Verschlüsselungsverfahren nicht geben kann. Theoretisch ist das auch
so. Praktisch aber reicht es schon aus, wenn die Berechnung von d aus e
einfach so langwierig ist, dass man se auch mit den schnellsten Computern
nicht innerhalb praktischer Zeitgrenzen durchführen kann. Das lässt sich mit
einer so genannten Einwegfunktion realisieren: Sie kann in eine Richtung (x
F--> y = f (x), also Ermittlung des Funktionswertes bei gegebenem x) leicht
berechnet werden, in die andere Richtung (y = f (x) H x) praktisch nicht.
Beispiel für eine Einwegfunktion ist die Zuordnung Name x - Telefonnummer f
(x) in einem Telefonfonbuch. Die eine Richtung ist kein Problem, nämlich zu
einem gegebenen Namen die zugehörige Telefonnummer zu finden. Die umgekehrte
Richtung, also zu einer gegebenen Telefonnummer den hörigen Namen zu finden,
dauert dagegen um ein Vielfaches länger!
Wo soll man aber eine solche Funktion hernehmen? Dazu hatten die
Mathematiker Ronald Rivest und Adi Shamir und der Computerwissenschaftler
Leonard Adleman Jahr 1978 die zündende Idee: Die Einwegeigenschaft des nach
ihnen benannten A-Verschlüsselungsalgorithmus beruht darauf, dass die
Multiplikation von Primzahlen fast keine Rechenzeit in Anspruch nimmt,
während aber die Zerlegung einer gegebenen Zahl in ihre Primfaktoren im
Vergleich dazu um ein Vielfaches länger benötigt! |
 |
Hier nun der RSA-Algorithmus, der die eingangs geforderten Eigenschaften
besitzt:
- Schlüsselerzeugung: Möchten Sie verschlüsselte Nachrichten empfangen,
so erzeugen Sie folgendermaßen einen öffentlichen und einen privaten
Schlüssel:
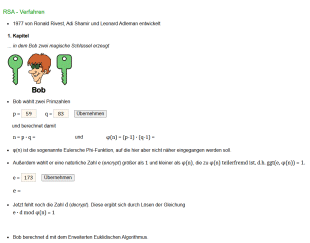
- wählen Sie zwei verschiedene Primzahlen p, q
- ermitteln Sie daraus die Zahlen n = p q und m = (p - 1) (q - 1)
- wählen Sie eine Zahl e, die teilerfremd zu m ist
- berechnen Sie die Zahl d, die e d = 1 (mod m) erfüllt (also das
multiplikative Inverse von e modulo m)
- geben Sie die Zahlen (n, e) als öffentlichen Schlüssel bekannt
- die Zahlen (n, d) behalten Sie als geheimen Schlüssel
- p, q und m werden nicht mehr benötigt (bleiben aber geheim!).
|
 |
Verschlüsselung: Wenn Ihnen nun jemand eine verschlüsselte Nachricht
schicken möchte, so schlägt er Ihren öffentlichen Schlüssel (n, e) nach,
verschlüsselt den Klartext x gemäß y = xe (mod n), und schickt den
Geheimtext y an Sie.
Die Verschlüsselungsvorschrift ist dabei eine Abbildung von 9d„ nach 9G„ und
die Entschlüsselungsvorschrift ist die zugehörige Umkehrabbildung.
Insbesondere muss also die Nachricht zuvor in eine Zahl kleiner als n
umgewandelt werden (bzw. in eine Anzahl von Blöcken, die kleiner als n
sind).
|
 |
Entschlüsselung:
Zum Entschlüsseln verwenden Sie Ihren geheimen Schlüssel
(n, d) und berechnen damit den Klartext gemäß
x = yd (mod n).
Dass wirklich yd = (XP)d = x`d(mod n) x gilt, ist an dieser Stelle noch
nicht unmittelbar einsichtig, kann aber mithilfe eines Satzes des
französischen Mathematikers Fernrat (Kleiner Fermat) bewiesen werden.
Natürlich ist es prinzipiell möglich, den geheimen Schlüssel (n, d) aus
Kenntnis des öffentlichen Schlüssels (n, e) zu berechnen, indem man die
Gleichung
e d = 1 (mod rri)
löst. Da aber m = (p - 1) (q - 1) geheim ist, muss man zur Ermittlung von m
zuerst die Primfaktoren p und q von n bestimmen. Sind die beiden
Primfaktoren geeignet gewählt (insbesondere genügend groß), so wird aber
auch der heutzutage schnellste Computer das Zeitliche segnen, bevor er mit
der Primfaktorzerlegung fertig ist. Die Sicherheit des RSA-Algorithmus
hängt also von der verwendeten Schlüssellänge ab (die der Größe der
Primzahlen entspricht). Das bedeutet natürlich, dass eine Schlüssellänge,
die heute als sicher gilt, aufgrund der steigenden Rechnerleistung in
einigen Jahren schon nicht mehr sicher ist!
Außerdem wäre es möglich, dass jemand einen schnelleren Algorithmus (der
polynomial von der Größe der Zahl n abhängt) zur Primfaktorzerlegung findet,
und in diesem Fall wäre die Sicherheit des RSA-Algorithmus endgültig dahin.
Mathematiker versuchen deshalb zu beweisen, dass es einen solchen
Algorithmus nicht geben kann.
Nun gleich zu einem Beispiel:
zum RSA-Rechner
Verschlüsselung mit dem RSA-Algorithmus
Die Nachricht „KLEOPATRA" soll mit dem RSA-Algorithmus verschlüsselt an
einen Empfänger geschickt werden, dessen öffentlicher Schlüssel (n, e)
(1147, 29 ist. Wandeln Sie zuvor die Nachricht so wie in Beispiel oben in
Ziffern um.
- wie lautet der Geheimtext?
- entschlüsseln Sie den Geheimtext (d = 149).
- versuchen Sie, den geheimen Schlüssel (n, d) aus der Kenntnis des
öffentlicher. Schlüssels (n, e) zu berechnen.
Lösung zu oben:
In Zahlen lautet KLEOPATRA: 11, 12, 5,15,16, 1,20,18, 1. Verschlüsseln
wir jede dieser Zahlen x gemäß y = x29 (mod 1147):
|
 |
|
 |
|
Abfolge für den RSA-Algorithmus ... |
|
Eingangsgrößen |
Chiffrierverfahren |
Dechiffrierverfahren |
Als Algorithmen werden benötigt:
- Modulo-Operationen
- Finden wirklich sehr große Primzahlen
- Teilbarkeitsregeln
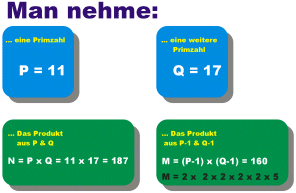
Als Größen müssen vereinbart werden:
- P (möglichst große Primzahl)
- Q (möglichst große Primzahl)
woraus resultieren:
- M (Produkt aus (P-1) und (Q-1))
- N (Produkt aus P und Q)
|
Als Algorithmen gehen ein:
- Wert für E
- Wert für M
- Beherrschen der Modulo-Operationen
Als Größen werden benötigt:
- Wert für E
- Wert für M
- Beherrschen der Modulo-Operationen
|
Als Algorithmen gehen ein:
- Modulo-Operationen
- Primzahlen
- Teilbarkeitsregeln
|
|
eine gute Möglichkeit, den RSA-Algorithmus zu verstehen |
|
 |
|
Vorbereitungen zum chiffrieren bzw.
Dechiffrieren ... |
- in der Praxis sind die festzulegenden Primzahlen P und Q groß,
ja sehr groß - wir sprechen von 100 und mehr Stellen
- sie stellen praktisch die Einwegfunktion dar - diese Zahlen zu
finden und miteinander zu multiplizieren, ist relativ einfach -
umgekehrt die Faktoren zu finden, praktisch nicht mehr möglich
- für unsere Demonstrationen verwenden wir nur relativ kleine
Primzahlen, da die Zwischenwerte auch damit schon enorm groß werden
- aus den ermittelten Primzahlen werden die Produkte N sowie mit
P-1 und Q-1 M
- N wird Bestandteil des "Public Keys"
- M wird in seine Primfaktoren zerlegt
- die Zahlen P und Q sind nach Abschluss aller Schritte für das
Chiffrierverfahren selbst nicht mehr von Bedeutung - sie bleiben aber
geheim!
|
- wir bestimmen in der Folge den Privat-Key- er muss geheim
gehalten werden
- dabei steht die Bezeichnung "E" für "encrypt" - entschlüsseln
- er ist in jedem Falle eine Primzahl im Bereich 2 ≤ E < M und
ist kein Primfaktor von M
- für das Beispiel P=11 sowie Q=17 und M=160 sowie N=187 mögliche
Werte:
3,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,102,
107,109,127,131,137,139,149,151,157 - dabei sind die Primfaktoren für
160 schon ausgelassen
|
- wir bestimmen in der Folge den Public-Key - er muss
veröffentlicht werden
- dabei steht die Bezeichnung "D" für "decrypt" - also
verschlüsseln
- er wird durch ein Produkt mit eines Zahl X mit M+1
dividiert durch E bestimmt
|
|
Bestimmung zweier Primzahlen P
sowie Q |

Generierung und Festlegung des "Encrypt"-Wertes
E - das ist der Private-Key |

Generierung und Festlegung des "Decrypt"-Wertes
D - das ist der Public-Key |
|
|
|
|
|
 |
|
 |
|
... und das Beispiel: |
|
Werte |
Alphabetische Zuordnung |
Encrypt - Chiffriren - also Verschlüsseln |
Decrypt - Dechiffriren - also Entschlüsseln |
- P = 11
- Q = 17
- N = 187
(Bestandteil des "Public- sowie des
Privat-Keys")
- M = 160
- E = 7
(Bestandteil des "Public-Keys")
- D = 23
(Bestandteil des "Privat-Keys")
|
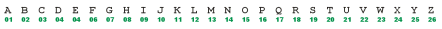
Zeichenpositionen im Alphabet |

Chiffrieren mit RSA |

Dechiffrieren mit RSA |
|
Plaintext zu Ciphertext |
|
Character |
A |
L |
L |
E |
S |
K |
L |
A |
R |
A |
U |
F |
D |
E |
R |
A |
N |
D |
R |
E |
A |
D |
O |
R |
I |
A |
|
Plain |
01 |
12 |
12 |
05 |
19 |
11 |
12 |
01 |
18 |
01 |
21 |
06 |
04 |
05 |
18 |
01 |
14 |
04 |
18 |
05 |
01 |
04 |
15 |
18 |
09 |
01 |
|
RSA |
01 |
177 |
177 |
146 |
145 |
88 |
177 |
01 |
171 |
01 |
98 |
57 |
115 |
146 |
171 |
01 |
108 |
115 |
171 |
146 |
01 |
115 |
93 |
171 |
70 |
01 |
|
... mit den obigen Zahlen einmal den
RSA zum Chiffrieren nachvollzogen - bewusst mit kleinen Zahlen :-)
|
Ciphertext zu Plaintext |
|
RSA |
01 |
177 |
177 |
146 |
145 |
88 |
177 |
01 |
171 |
01 |
98 |
57 |
115 |
146 |
171 |
01 |
108 |
115 |
171 |
146 |
01 |
115 |
93 |
171 |
70 |
01 |
|
Plain |
01 |
12 |
12 |
05 |
19 |
11 |
12 |
01 |
18 |
01 |
21 |
06 |
04 |
05 |
18 |
01 |
14 |
04 |
18 |
05 |
01 |
04 |
15 |
18 |
09 |
01 |
|
Character |
A |
L |
L |
E |
S |
K |
L |
A |
R |
A |
U |
F |
D |
E |
R |
A |
N |
D |
R |
E |
A |
D |
O |
R |
I |
A |
|
... mit den obigen Zahlen einmal den
RSA zum Dechiffrieren nachvollzogen - bewusst mit kleinen Zahlen :-) |
 |
|
 |
Hier hat uns Herr Rainer Gürth auf der Informatiklehrerkonferenz am
12.11.05 in Dresden einige unschlagbar wertvolle Tipps zu Arbeit gegeben und
diese Materialien großzügigerweise verfügbar für unsere Unterrichtsarbeit
gemacht. |
 |
|
 |
|
