Blowfish

Letztmalig dran rumgefummelt: 08.06.20 14:53:19

	DES, der Data Encryption Standard, ist ohne Frage das am besten untersuchte kryptografische Verfahren. Er stellt ein symmetrisches Verfahren dar. Modernen Entwurfsprinzipien und moderner Kryptanalyse haben wir wesentlich diesem
	1. Zur Geschichte 2. Zum Verfahren 3. Einzelbereiche sowie deren Details 4. Triple DES 5. Softwarebereich 6. Verwandte Bezüge
	RSA-Verfahren & Einwegfunktionen International Data Encryption Algorithm inhaltlich auf korrektem Stand - evtl. partiell unvollständig ;-) Informatik-Profi-Wissen
	Schlüsselbuch   was bietet der DES auch heute noch? symmetrischer Blockalgorithmus (heute mögliche Blocklänge theoretisch frei definierbar (in sinnvollen Grenzen die liegen heute hardwaremäßig definierbar bei über 216 Bit) derzeitige Schlüssellänge: definiert auf 56 Bit - einfach erweiterbar auf 128, 192 und 256 Bits) als Triple DES auch mit 56 Bit resistent gegen alle bisher bekannten Attacken Performance und Kosten  extrem gering - auf Micrcontrollern sowie Hardware leicht implementierbar in Hardware gegossen extrem schnell in einfachster Hardware realisierbar (Fangregister, Schieberegister sowie Logik - vor allem XOR) patentfrei und weltweit kostenlos nutzbar äußerst flexibel - verschiedene Plattformen möglich (z.B. 8-Bit-Prozessoren auf Smart Cards), anpassbar, einfach)
	Quellen: Kryptografie für Dummies Seite 44 ff. Kryptographie verständlich  Seite 63 ff. Angewandte Kryptographie Seite 59 ff. KRYPTOGRAFIE Verfahren  · Protokolle · Infrastrukturen Seite 85 ff. Abenteuer Kryptologie - Methoden, Risiken und Nutzen der Datenverschlüsselung Seite 117 ff.
	https://de.wikipedia.org/wiki/Data_Encryption_Standard

1. Zur Geschichte

	Lucifer - das Vorgeplänkel zum DES! Dabei ging es, wie bei allen noch folgenden binären Chiffres zum ersten mal um eine völlig neues Konzept auf Basis des Vernam-Chiffres, welcher wiederum den Baudot-Code als Basis hatte.  Ursprung war die Erkenntnis, dass alle bisher im Einsatz befindlichen "Konfusionsverfahren" im großen technischen Stil nicht verwendbar waren, da bereits nachweislich durch Computereinsatz kompromittiert. Das DES-Verfahren - ein Quasi- sowie Basis-Standard der modernen Blockchiffre - was bedeutet dies?
	... Basis des DES-Algorithmus ist das Projekt Lucifer sowie der VERNAM-Chiffre.
	... ????
	... ???
	???

2. Zum Verfahren

	… bereits Claude Shannon forderte, dass der Geheimtext durch Konfusion und Diffusion aus dem Klartext gebildet wird. Konfusion bedeutet in etwa Mischen, das heißt, die statistischen Eigenschaften des Chiffretextes sollten möglichst gut einer Folge aus Zufallszahlen gleichen, auch wenn der Klartext stark strukturiert ist. Diffusion bedeutet, dass jedes Klartextbit auf möglichst viele Chiffretextbits verteilt wird. Damit werden Angriffe erschwert, die auf der Zuordnung eines Klartextteiles zu einem bestimmten Chiffretextteil und dem Schlüssel basieren. Als ein vernünftiger Kompromiss aus Diffusion und Effizienz der Implementierung werden heute meist Blocklängen von 64 oder 128 Bit gewählt. Bevor wir nun auf die Details bestimmter Blockchiffren eingehen, wollen wir einige allgemeine Überlegungen anstellen. Um eine möglichst hohe Sicherheit zu erreichen, wäre es wünschenswert, den Schlüsselraum so groß wie möglich zu machen. Dies ist leider nicht möglich, denn die Gesamtzahl aller Chiffren mit einer Blocklänge von 64 Bit beträgt 264! (Fakultät!). Um eine spezielle Chiffre zu codieren wird also ein Schlüssel der Länge 1092264) das sind ~ 270 sind rund 2 *1021 Bit benötigt. Das sind etwa 1011 GByte. Um einen einzigen derartigen Schlüssel zu speichern, würde man mehr als 109 Festplatten mit einer Kapazität von je 100 GByte benötigen, die zusammen etwa 500 000 Tonnen schwer wären. Man wird sich also in der Praxis auf eine kleine Teilmenge von Blockchiffren mit kurzem Schlüsselbeschränken, die Diffusion und Konfusion möglichst gut realisieren.
	CCITT     ASCII-Codes   8-Bit Lochstreifen   8-Bit-Lochstreifen von Emely Arlt mit Arbeitsstand 29.11.2019 (ACHTUNG: nur Standardzeichen sind implementiert!!!) ... als startbare Datei ... als ZIP-Archiv
	wir reden von einem symmetrischen monoalphabetischen Blockchiffre (Entschlüsseln funktioniert genau so wie verschlüsseln - und: es gibt nur einen Schlüssel!) Konfusion sowie Diffusion sind die Hauptprinzipien nach der Zeichenkonvertierung läuft alles auf Gruppen von jeweils 8 Bit - ist der Datenstrom größer, wird auf immer 8 Zeichengruppen aufgefüllt verschlüsselt werden jeweils Gruppen (Blockchiffre) zu immer 8 × 8 Bit bedingt durch die Verarbeitung von Bits lässt sich das gesamte Verfahren in Hardware gießen - streng genommen nichts weiter als Fangregister kombiniert mit Decodern sowie Schieberegistern ... denn: nichts ist schneller als Hardware interessant ist, dass an den Schlüssel streng genommen nur eine einzige Bedingung gestellt werden muss: er muss geheim bleiben!!! es gibt schwache Scllüssel - alles 0 sowie alles 1
	... raffiniert auf direkter IC-Ebene: ein Feistel-Netzwerk ... DES auf Silizium - das gibt es heute nur noch als Einzelbauelemente - die sind jedoch immer noch verfügbar ;-) DES-Logik Feistelnetzwerk pics/data_encryption_standard/des_chip01.jpgDES-Chip   Logische Struktur des DES-Chips
	DES, der Data Encryption Standard, ist ohne Frage das am besten untersuchte kryptografische Verfahren mit dem Chararkter eines monoalphabetischen sowie symmetrischen Verfahrens – geht ja eigentlich gar nicht – ist ja bewiesenermaßen TOP-unsicher und leicht angreifbar Moderne Entwurfsprinzipien und moderne Kryptanalyse haben wir aber trotzdem wesentlich diesem Algorithmus zu verdanken. Obwohl der Verdacht, die NSA könnte in DES eine Hintertür eingebaut haben, nie ganz ausgeräumt werden konnte, aktuell bis heute kein praktisch wirklich verwertbarer Angriffspunkt gefunden worden. Die Unsicherheit von DES rührt daher, dass der Brute-Force-Angriff heutzutage technisch möglich geworden ist!!! DES spielte in der Geschichte und auch heute noch eine überragende Rolle – mit Triple-DES gibt es ja auch bereits eine zukunftweisende Alternative
	Encoding Standard-DES Decoding Standard-DES Encoding des DES-Block-Chiffre Download im CorelDraw 11.0-Format Decoding des DES-Block-Chiffre Download im CorelDraw 11.0-Format

3. Technische Details

	Also grundsätzlich ist der DES ganz einfach: 64 Eingangsbits sowie 56 Keybits kommen in einen Mixer und herauskommen 64 Cipherbits. Beim Entschlüsseln lässt man den Mixer nur einfach umgekehrt laufen und kann alles wieder lesen!!! Um dies zu realisieren, wird der Eingabetext Blöcke zu je acht Zeichen zerlegt (notfalls werden ergo in der letzten Gruppe Dummy-Zeichen angefügt) Das funktioniert für alles, was im ASCII- Code zwischen 32D und 255D liegt. Alles nachfolgend aufgezeichnete bezieht sich also immer auf jeweils Gruppen zu 8 mal 8 Bit.
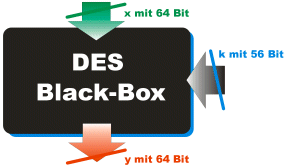
	Strategie des DES-Algorithmus (...und alles, was wir im Augenblick nicht genau wissen, erklären wir zu einer "Black-Box"!) ... die Grundprinzipien des DES ... das Rundenverfahren des DES ... die F-Funktion ... die Substitutions-Boxen (kurz: S-Boxen) ... das Key-Konzept Basisfunktion des DES Download im CorelDraw 11.0-Format
	C- sowie D-Keyblock rotieren nach jeder Nutzung getrennt um jeweils 1 oder 2 Bit
	Unser Beispiel zum Verschlüsseln: Plaintext mit 8 Zeichen Länge: PASSWORD Plaintext im ASCII-Code - jeweils dreistellig: 080 065 083 083 087 079 082 068 Plaintext im Binär-Code - jeweils 8 Bit pro Zeichen: 01010000 01000001 01010011 01010011 01010111 01001111 01010010 01000100 56-Bit Key: 1100111 0100001 1011111 0011001 1000011 1001011 0011110 0101011 - 56-Bit Key mit Leerezeichen getrennt: 11001110100001101111100110011000011100101100111100101011
	... mein 8-Zeichen-Beispiel ... mein 8-Zeichen-Beispiel - aufbereitet in Bits ... die Bits - nur anders angeordnet ... die Eingangspermutation ... mein Plaintext-Beispiel
	Encryption zerfällt grundsätzlich in zwei Teile: Plaintext-Konvertierung sowie Key-Permutationen Plaintext-Aufbereitung Key-Aufbereitung Bitanordnung des ersten 8 * 8 Zeichen-Musters 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 Bitanordnung nach der Eingangspermutation 58 50 42 34 26 18 10 02 60 52 44 36 28 20 12 04 62 54 46 38 30 22 14 06 64 56 48 40 32 24 16 08 57 49 41 33 25 17 09 01 59 51 43 35 27 19 11 03 61 53 45 37 29 21 13 05 63 55 47 39 31 23 15 07 ... gefunden in: https://www.cs.uni-potsdam.de/ti/lehre/04-Kryptographie/slides/DES-AES  Seite 6 8 × 7 Key-Bits - also der Schlüsselstrom 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 ... das ist die Schlüsselmenge in 7-Bit-Gruppen, welche wirklich nach Protokoll verwendet wird ... ursprünglich nach IBM-Empfehlung 128 Bit - das wäre eine wesentlich höhere Sicherheit 7 Key-Bits + Parity-Bit 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 ... das 8. Bit dient nur der Absicherung der Nachrichtenverbindung - und wird nach erfolgreichem Eintreffen sofort wieder gelöscht die weitere Nummerierung erfolgt trotzdem auf deren Anwesenheit als Basis, denn sie sind ja erst einmal da ;-)
	... die Ausgangs-Permutation     Bitanordnung Ciphertext nach der 64 Bit Ausgangspermutation         40 08 48 16 56 24 64 32 39 07 47 15 55 23 63 31 38 06 46 14 54 22 62 30 37 05 45 13 53 21 61 29 36 04 44 12 52 20 60 28 34 02 42 10 50 18 58 26 33 01 41 09 49 17 57 25 ... gefunden in: Kryptographie verständlich  Seite 71
	Decryption zerfällt ebenfalls in grundsätzlich zwei Teile: Key-Aufbereitung Decryption

4. Triple DES

Die Sicherheit ist heutzutage aus gutem Grunde vor allem für sensible sowie regelmäßig anfallende Datenübertragungen mit hohem  Risikopotential in Frage gestellt. Vor allem der heute in der Bitanzahl 56 geltende Schlüssel ist als "schwach" einzustufen. Man könnte den Schlüssel stärken 256 Bit sind auch heute noch absolut hart für einen Brute-Force-Angriff. Dies würde allerdings bedeuten, ein bestehendes sowie gut Bekanntes System wieder obsolet zu stellen - der einfachere Weg lautet folgerichtig: wir machen das Ganze drei Mal (... das gilt bis heute auch gegen Angriffe von Parallelrechnersystemen als resistent)!

Arbeitsstand per 21.3.2020

5. Software-Lösungen

	Drei Lösungsansätze kommen in Frage. Delphi-Programme mit dem Vorteil, dass schnell auch größere Texte ver- bzw. entschlüsselt werden können, ECEL hat den Vorteil, dass man für eine 8 × 8-Matrix die Arbeitsweise schnell und gut sehen kann. Eine Hardware-Simulation mit Profi-Lab 4.0 hier ist die Logik der Permutatonen gut erkennbar.
	EXCEL-Lösung - hat die besten Aussichten auf eine vollständige Lösung in absehbarer Zeit!!! Konvertierung des Eingabetextmusters in Bitgruppen Plaintext-Aufbereitung mit Eingangspermutation sowie Aufspalung in zwei 32-Bit-Blöcke ... jeder Block wird durch Mehrfachnutzung einzelnerr Bits auf 48 Bit erweitert Key-Konvertierung   Pflichteingabe von 8 definierten ASCII-Code relevanten Zeichen       Download Kalkulationstabelle
	Profi-Lab 4.0 ProfiLab 4.0-Projekt März 2020           Eingabemaske Encoding Download Anwendung

6. Verwandte Themen

	... Grundprinzip der Gesamtausschreibung war ja, dass sich alles relativ einfach in Hardware gießen lässt. Also die Eingaben via ASCII in Bits zerlegen und mit diesen dann die gesamte Verschlüsselung durchführen. Das bedeutet, dass wir hier eben auch zwangsläufig die Hardware tangieren. Das Prinzip war ja: kein Eingriff menschlicher Hand, extrem sicher und vor allem wahnsinnig schnell.
	Schieberegister Schieberegister Bifid-Chiffre VIC-Chiffre Doppelwürfel Dr. Richard Sorge

zur Hauptseite

© Samuel-von-Pufendorf-Gymnasium Flöha

© Frank Rost am 8. Juni 2020 um 16.14 Uhr