McCarthy-Funktion history menue Letztmalig dran rumgefummelt: 30.05.12 16:45:25

Amerikanischer Mathematiker, der in den 50er Jahren die Programmiersprache LISP implementiert hat. Diese Funktion ist neben einigen anderen bis heute unschlagbar als Anwendung zum Erlernen rekursiver Denkstrukturen. - und genau deshalb nehmen wir sie hier auseinander ;-)
1. Problembeschreibung
2. Hintergründe und Zusammenhänge - Einordnung in Klassen
3. Lösungsalgorithmen
4. Programmvorschläge
5. Zusammenfassung
6. Weiterführende Literatur
7. Linkliste zum Thema

die Informatikseiten

Logo für die Mc Carthy-Funktion

inhaltlich auf korrektem Stand - evtl. partiell unvollständig ;-)

Informatik-Profi-Wissen
Beachte vor allem bei Problemlösungsalgorithmen: Murphys Gesetze sowie deren Optimierung durch Computer sowie deren Optimierung durch Computer

1. Problembeschreibung history menue scroll up

Nach Durchlaufen endlich vieler Zwischenschritte wird 91 erreicht und ist nicht mehr weiter zu vereinfachen, da sich die Funktionen dann unendlich lange selbst gegenseitig aufrufen. McCarthy terminiert nicht!

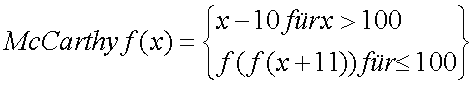Die McCarthy-Funktion

mit 1 <= x <= 101
 

2. Hintergründe, Zusammenhänge - Einordnung in Klassen history menue scroll up

Der Lösungsalgorithmus für die McCarthy-Funktion
effiziente Lösung nur als rekursiver Algorithmus
gegenseitige Rekursion - die Funktionen für größer 100 und kleiner 100 für die Zwischenwerte rufen sich gegenseitig auf
 

3. Lösungsalgotihmus history menue scroll up
Wenn es mindestens einen Lösungsansatz gibt, dann versuche, aus den gegebenen Wortpaaren identische Sätze auf beiden Seiten der Gleichung zu bilden. Wiederhole dies solange, bis keine weitere Möglichkeit mehr existiert.

McCarthy für x=1

f(1)=1+11=f(f(12))

f(12)=12+11=f(f(23))

f(23)=23+11=f(f(34))

f(34)=34+11=f(f(45))

f(45)=45+11=f(f(56))

f(56)=56+11=f(f(67))

f(67)=67+11=f(f(78))

f(78)=78+11=f(f(89))

f(89)=89+11=f(f(100))

f(100)=100+11=f(f(111))

f(111)=111-10=101

f(101)=101-10=91
McCarthy für x=5

f(5)=5+11=f(f(16))

f(16)=16+11=f(f(27))

f(27)=27+11=f(f(38))

f(38)=38+11=f(f(49))

f(49)=49+11=f(f(60))

f(60)=60+11=f(f(71))

f(71)=71+11=f(f(82))

f(82)=80+11=f(f(93))

f(93)=93+11=f(f(104))

f(104)=104-10=94

f(94)=94+11=f(f(105))

f(105)=105-10=95

f(95)=95+11=f(f(106))

f(106)=106-10=96

f(96)=96+11=f(f(107))

f(107)=107-10=97

f(97)=97+11=f(f(108))

f(108)=108-10=98

f(98)=98+11=f(f(109))

f(109)=109-10=99

f(99)=95+11=f(f(110))

f(110)=110-10=100

f(100)=100+11=f(f(111))

f(111)=111-10=101

f(101)=101-10=91

4. Programmvorschläge history menue scroll up

Was auch immer ich tue, muss ich rekursiv lösen und die Mächtigkeit schon für kleine Argumente ist durch die Anzahl der Zwischenwerte enorm. Auch wird eine extreme Rekursionstiefe erreicht und somit der Speicher maximal ausgelastet. Effizient ist die Abarbeitung aber trotzdem noch, da keine weitere Lösungsmöglichkeit existiert.

Die nachfolgend beschriebene Lösung wurde mit Turbo-PASCAL 7.0 erstellt

FUNCTION mc_carthy__kleiner_100 (up_zahl:BYTE):BYTE;

BEGIN{begin mc_carthy__kleiner_100}
  IF up_zahl<=100
   THEN
  BEGIN{begin of then}
      mc_carthy__kleiner_100:=mc_carthy__kleiner_100(mc_carthy__kleiner_100(up_zahl+11));
  END{end of then}
  ELSE
  BEGIN{begin of else}
    mc_carthy__kleiner_100:=up_zahl-10;
  END;{end of else}
END;{end of mc_carthy__kleiner_100}

FUNCTION mc_carthy__groesser_100 (up_zahl:BYTE):BYTE;

BEGIN{begin mc_carthy__groesser_100}
  mc_carthy__groesser_100:=up_zahl-10;
END;{end of mc_carthy__groesser_100}
 
 

5. Zusammenfassung history menue scroll up

Hier greifen wir unter anderem die Argumente für einen Algorithmus auf und vergleichen, ob Übereinstimmung in allen Punkten gegeben ist.
Endlichkeit der Beschreibung ist gegeben
Eindeutigkeit ist gegeben - jeder Schritt ist für jede Bedingung eindeutig fest vorgegeben und lässt keine Abweichung zu
Effektivität ist gegeben - jeder Schritt ist ausführbar
Terminierung ist nicht gegeben - der Algorithmus läuft nach erreichen des Zwischenergebnisses 91 ewig und generiert einen Stapelüberlauf
Determiniertheit ist gegeben, der Folgeschritt nach einer Operation ist immer bekannt

6. Weiterführende Literatur history menue scroll up

 
der Lösungsalgorithmus der Türme von Hanoi ist nicht komplex, jedoch schon mit geringer Anzahl n mächtig
es muss also insgesamt hoher Lösungsaufwand betrieben werden - auch ein Computer wird für n=1000 in absehbarer Zeit keine Lösung bringen
 

7. Links zum Thema history menue scroll up

Viele gibt es - die meisten sind JAVA-basierte Spiele, um den erkannten Lösungsalgorithmus nach zu vollziehen. Wie gesagt, wenn Du vor hast, das Spiel noch am laufenden Tag zu beenden, verwnde keine Scheibenzahl größer 20 - das ist dann schon nicht mehr zu schaffen.
http://www.panix.com/~derwisch/hannes/elug/lisp/scheme.pdf
http://www-is.informatik.uni-oldenburg.de/~dibo/teaching/java9900/vorlesungen/vorlesung7/tsld031.htm
http://www.lexikon-definition.de/LISP.html


zur Hauptseite		 © Samuel-von-Pufendorf-Gymnasium Flöha © Frank Rost im August 1995

... dieser Text wurde nach den Regeln irgendeiner Rechtschreibreform verfasst - ich hab' irgendwann einmal beschlossen, an diesem Zirkus nicht mehr teilzunehmen ;-)

„Dieses Land braucht eine Steuerreform, dieses Land braucht eine Rentenreform - wir schreiben Schiffahrt mit drei „f“!“

Diddi Hallervorden, dt. Komiker und Kabarettist

Diese Seite wurde ohne Zusatz irgendwelcher Konversationsstoffe erstellt ;-)