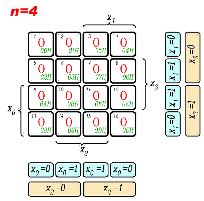
Logik-Projekt F. Rost im Dezember 2019 auf der Grundlage von Vorleistungen aus den Jahren 2013 sowie 2014
... resultierende Logik-Gleichung
y0 = x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0
y1 = x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0
| Hintegrundwissen sowie Tools für die Karnough-Veitch-Tafeln | ... die zugeordnete 5-Eingangs-Matrix nach Karnaugh/Veitch für beide Ausgänge | ... die sich ergebende Minimal-Logik nach Karnaugh/Veitch | ||||
|
Achtung - per 30.12.2019 sind diese Gleichungen noch nicht zusammengafasst y0 = x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 y1 = x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 ˅ x4 x3 x2 x1 x0 |
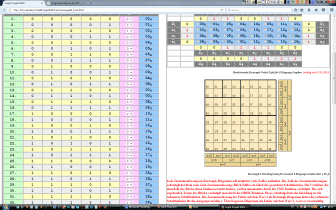
| Karnaugh-Veitch-Diagramm für n=5 - die Tafel für y0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vorgegebene Logiktabelle ... vier mal ist der Ausgang auf 1 gesetzt
|
Resultierende Karnaugh-Veitch-Tafel für 5-Eingangs-Logiken (richtig seit 18.11.2012)
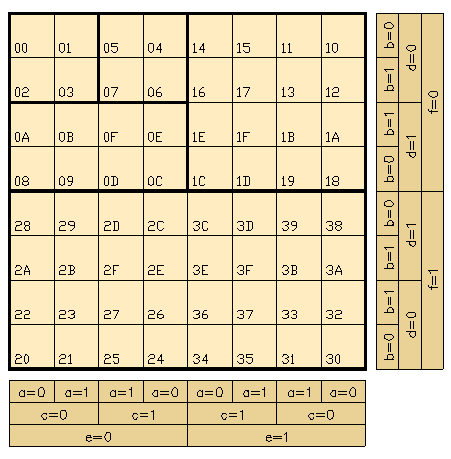
Karnaugh-Veich-Diagramm für maximal 6 Eingangsvariable (hier a bis f) Jede Zusammenfassung im Karnaugh-Diagramm soll möglichst viele Felder enthalten. Die Zahl der Zusammenfassungen soll möglichst klein sein. Jede Zusammenfassung (Block) bildet ein Glied der gesuchten Schaltfunktion. Die Variablen, die innerhalb des Blocks ihren Zahlenwert nicht ändern, werden miteinander durch die UND-Funktion verknüpft. Die sich ergebenden Terme der Blöcke verknüpft man durch die ODER-Funktion. Diese schaltalgebraische Gleichung ist die reduzierte Schaltfunktion. Die Zusammenfassung der Felder mit dem Wert 1 im Karnaugh-Diagramm liefert die reduzierte Schaltfunktion für die Ausgangsvariable s. Überwiegen im Diagramm die Felder mit dem Wert 1, so ist es zweckmäßig durch Blockbildung der Felder mit dem Wert 0 den Wert s der Ausgangsvariablen zu ermitteln. Durch nochmaliges Negieren von s erhält man dann den Wert s der Ausgangsvariablen.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
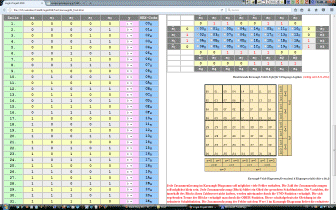
| Karnaugh-Veitch-Diagramm für n=5 - die Tafel für y1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Vorgegebene Logiktabelle ... fünf mal ist der Ausgang auf 1 gesetzt
|
Resultierende Karnaugh-Veitch-Tafel für 5-Eingangs-Logiken (richtig seit 18.11.2012)
Karnaugh-Veich-Diagramm für maximal 6 Eingangsvariable (hier a bis f) Jede Zusammenfassung im Karnaugh-Diagramm soll möglichst viele Felder enthalten. Die Zahl der Zusammenfassungen soll möglichst klein sein. Jede Zusammenfassung (Block) bildet ein Glied der gesuchten Schaltfunktion. Die Variablen, die innerhalb des Blocks ihren Zahlenwert nicht ändern, werden miteinander durch die UND-Funktion verknüpft. Die sich ergebenden Terme der Blöcke verknüpft man durch die ODER-Funktion. Diese schaltalgebraische Gleichung ist die reduzierte Schaltfunktion. Die Zusammenfassung der Felder mit dem Wert 1 im Karnaugh-Diagramm liefert die reduzierte Schaltfunktion für die Ausgangsvariable s. Überwiegen im Diagramm die Felder mit dem Wert 1, so ist es zweckmäßig durch Blockbildung der Felder mit dem Wert 0 den Wert s der Ausgangsvariablen zu ermitteln. Durch nochmaliges Negieren von s erhält man dann den Wert s der Ausgangsvariablen.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||