3.6. Ellipsenkonstruktionen

Letztmalig dran rumgefummelt: 21.10.06 00:37:23

	Lange Zeit galt auch schon von der Mythologie her der Kreis als vollkommen 8ist er ja auch), und es dauerte recht lange, bis man erkannte, das der Kreis nichts weiter als ein Spezialfall einer viel allgemeineren Fläche ist: der Ellipse!
	1. mit konzentrischen Kreisen   2. Klassische Geometrie für Ellipsen   3. Kreis in zwölf gleiche Abschnitte teilen   4. Teilen einer Strecke AB in n gleiche Teile   5. Programm ausführen
	die Übungsserie zu diesem Komplex einschließlich Lösungen gibt's hier

1. Mit konzentrischen Kreisen

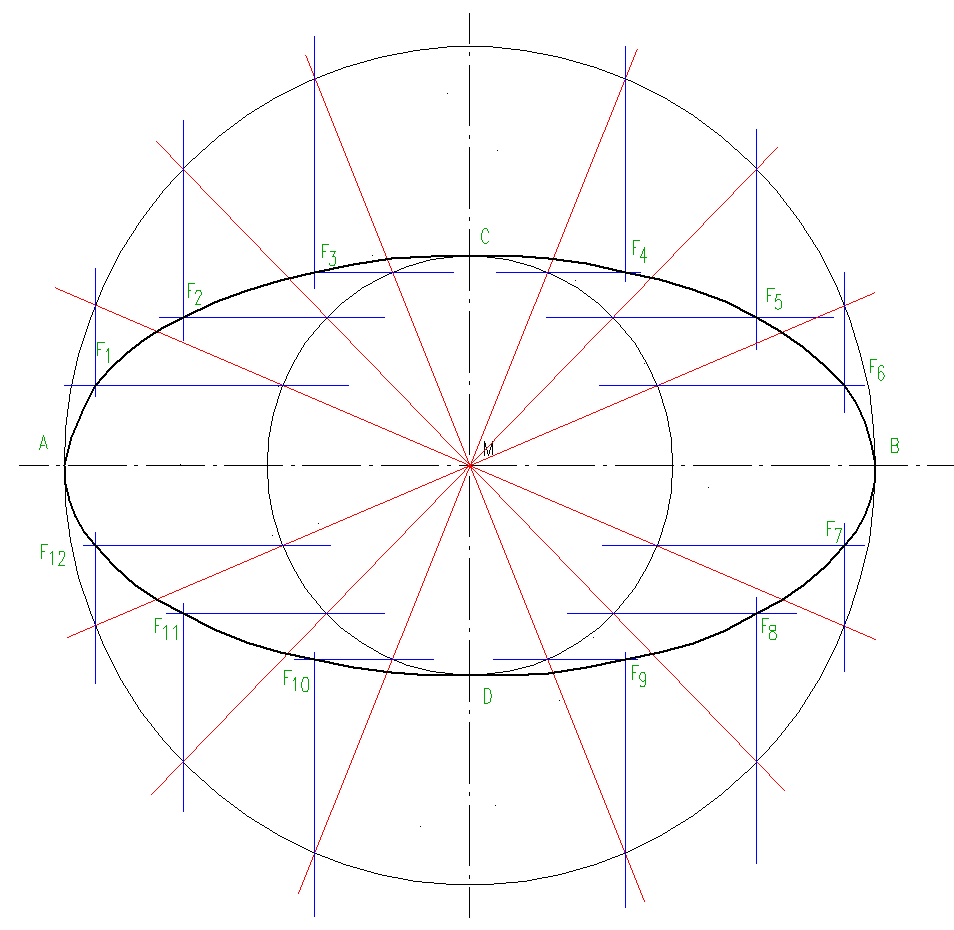
	__ AB entspricht großer Ellipsenachse
	__ CD entspricht kleiner Ellipsenachse
	__                __ man zeichnet um den Mittelpunkt M zwei konzentrische Kreise mit den Radien ½ AB sowie ½ CD
	unter theoretisch beliebigem Winkel werden mehrere Durchmesser abgetragen (je mehr, desto genauer der Kurvenverlauf - also ergeben unendlich viele Durchmesser die genaue Ellipse)

2. Kreismittelpunkt suchen

schlägt man um die Punkte A, B, C und D eine Kreisbogen mit dem Radius r in beiden Richtungen, so erhält man die Teilungspunkte auf der Peripherie des Kreises

3. Kreis in zwölf gleiche Abschnitte teilen

	man ziehe durch den Punkt A der Strecke AB eine Hilfsgerade unter beliebigem Winkel größer 0° bezogen auf Strecke AB
	nun trage auf der Hilfsgeraden beginnend in Punkt A den beliebigen Radius r n-mal ab (wobei n der Faktor der Streckenteilung ist)
	aus dem letzten Schnittpunkt mit der Hilfsgeraden ergibt sich Punkt C, welcher mit Punkt B zu verbinden ist
	die Streckenteiler ergeben sich jeweils aus Parallelen der Strecke CB in die einzelnen Radienschnittpunkte auf der Hilfsgeraden

4. Kreis in zwölf gleiche Abschnitte teilen

 

	um den Punkt C wird ein Kreisbogen mit beliebigem Radius unter der Bedingung geschlagen, dass die Gerade g zwei mal geschnitten wird
	dadurch entstehen die Schnittpunkte D sowie E
	um die Punkte D und E wird wiederum ein Kreisbogen mit Radius r aus dem ersten Schritt geschlagen - es entsteht Schnittpunkt F
	die Verbindung von C mit F ergibt das gewünschte Lot

zur Hauptseite

© Samuel-von-Pufendorf-Gymnasium Flöha

© Frank Rost im August 2003