4.1. Knobelaufgabe 5
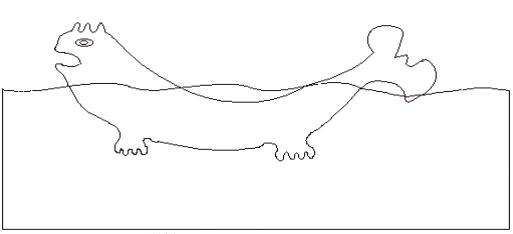
In dieser Aufgabe benötigen wir wieder den Graph des staunenden Seeungeheuers.
Überlege dir einmal, dass bei jedem Bild, in dem von jedem Knoten immer eine gerade
Kanten Anzahl ausgeht, die Anzahl der unbeschränkten Kanten auch gerade ist!
Den nun erhaltenen Graphen zerlegen wir in geschlossene Kantenzüge. Dazu starten
wir an einem Knoten, folgen einer von ihm ausgehenden Kante bis zum nächsten
Knoten. Dort wählen wir eine Kante aus, die noch nicht durchlaufen wurde. Das geht
so weiter, bis der Startknoten wieder erreicht wird. Das fortschreiten an den Knoten
ist gesichert, da von ihnen eine gerade Anzahl von Kanten ausgeht. Wenn du alle
Kanten des Graphen in geschlossenen Kantenzügen erfasst hast, so zähle, wie viele
dieser Kantenzüge jedes Flächenstück umgeben.
In dieser Abbildung sind die Knoten (A,
B, C...)
wieder blau und die Kanten ( 1, 2, 3...) rot
eingezeichnet.
Von allen Knoten führen vier Kanten weg. Zwischen jeweils zwei Knoten, liegt immer
mindestens ein geschlossener Kantenzug. Zwischen A
und B, B
und C, D
und E, E
und F, liegen jeweils zwei geschlossene
Kantenzüge (und zwar : A -
1 + 16 -
B , B -
2 + 15 -
C , D -
4 + 12 -
E , E -
5 + 13 -
F ).
Mein Startknoten ist der Knoten A, von ihm
aus wollte ich über alle Knoten und Kanten wieder zu ihm zurück finden. Von ihm
aus verläuft mein Weg über die Kante 1 zum
Knoten B. (Ich habe die Kanten gleich in der
Reihenfolge meines Weges nummeriert, zum besseren Verständnis). Weiter verläuft
er über Kante 2 zu Knoten
C. Von dort aus in Richtung D über
Kante 3. Als nächstes zu
E über 4. Dann zu
F über 5. Über
6 zu G. Vom Knoten
G aus über die Kante 7 zum Knoten
H. Dort angekommen zu
I über 8 und zu
J über 9. Danach bin ich über die Kante
10 zum Anfangsknoten
A gekommen, aber ich habe bemerkt, dass ich noch längst nicht alle
Linien durchlaufen hatte. Also beschloss ich mich über 11 zum Knoten D zu gehen . Dann über 12 zu
E, über 13 zu F und dann von
F aus über 14 zu C
zu gelangen. Dort weiter zu B
über 15. Und als Endspurt über 16 zum Ausgangspunkt
A.
Ich habe also alle Kanten durchlaufen, bin an meinem Startknoten zum Ende wieder
angekommen, und bin keine Kante doppelt gegangen.
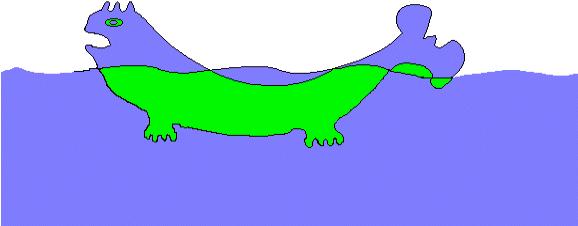
Nun stellt sich die Frage, reichen 2 Farben aus um das Seeungeheuer auszumalen,
so dass man noch alle Kanten erkennt?
Wie du sehen kannst, ist dies möglich!
Doch reichen immer zwei Farben?
Sie reichen stets dann, wenn im zugeordneten Graphen von jedem Knoten eine gerade Anzahl von Kanten ausgeht. (So wie es im Graphen des Seeungeheuers der Fall war!)
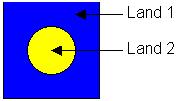
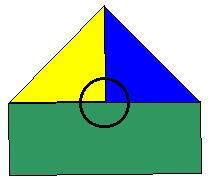
Ist die Anzahl der Kanten von einem Knoten ungerade, z. B. 3, so kannst du dich
leicht anhand einer Skizze davon überzeugen, dass zwei Farben allein nicht genügen.
Denn in dieser Abbildung musste man drei Farben verwenden, weil von einem Knoten
(blau eingekreist) drei Kanten verlaufen.
Doch nun bleibt noch die Frage offen, wie viele Farben man mindestens benötigt,
um eine beliebige Abbildung auszumalen. Wir wissen jetzt, dass zwei nicht reichen.
Aber müssen es 18 sein oder nur Zehn? Oder gar nur sechs?
Das Problem tritt ebenso beim Färben von politischen Landkarten auf. Länder mit
einer gemeinsamen Grenze müssen unterschiedliche Farben erhalten. Natürlich treten
hier keine unbeschränkten Grenzen auf. (Da gäbe es ja ein Land im Land).
Außerdem wollen wir vereinfachend annehmen, das jedes Land zusammenhängend ist,
also keine Inseln oder Gebiete inmitten anderen Ländern besitzt. Das Problem wird
auch nicht komplizierter, wenn Länder völlig von anderen oder vom Meer eingeschlossen
sind. Diese Teile der Karte können nämlich als extra zu färbende Karte aufgefasst
werden.
Treffen mehr als zwei Länder in einem Punkt aneinander, so heißt dieser Punkt
"Ecke".
Von einer Ecke gehen also mindestens drei Kanten aus.
Willst du heraus finden, wie viele Farben man mindestens für jede beliebige Abbildung
braucht? Dann gehe am besten gleich zur Seite "Fünf Farben
reichen immer ?".
 Ein Seeungeheuer staunt
Ein Seeungeheuer staunt
 Zurück zur Gliederung
Zurück zur Gliederung


 Ein Seeungeheuer staunt
Ein Seeungeheuer staunt Zurück zur Gliederung
Zurück zur Gliederung