1.1. Knobelaufgabe 1
Ihr kennt doch sicherlich alle die Geschichte, in der ein Fährmann vor dem Problem
stand, einen Kohlkopf, eine Ziege und einen Löwen über einen Fluss zu transportieren.
Doch er konnte in seinem Boot immer nur Einen mitnehmen, sonst wäre es gesunken.
Auch durfte er nur Löwe und Kohlkopf allein an einem Ufer lassen, um ein Unglück
zu vermeiden. Denn wäre der Löwe mit der Ziege zusammen, würde er sie zerfleischen.
Und würde er die Ziege und den Kohlkopf unbeaufsichtigt lassen, würde die Ziege
natürlich einmal kosten wollen. Da stellt sich uns die Frage: Wie soll sich der
Fährmann verhalten?
Wir wollen an diese Aufgabe erst einmal logisch herantreten. Um den Sachverhalt
zu klären. Wir stellen uns vor wir ständen vor diesem Problem und befinden uns
an dem Ufer eines Flusses. Bei uns ist eine Ziege, ein Kohlkopf und ein Löwe.
Was würdest du tun?
Ich habe einen guten Weg gefunden, und den will ich euch anhand von ein paar
lustigen Bildchen erklären. So, kann's losgehen?
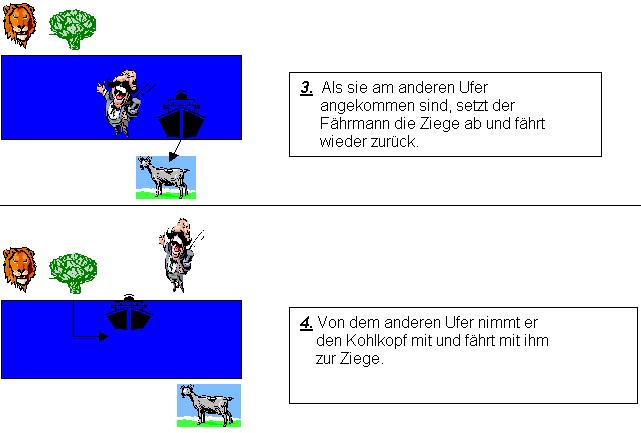
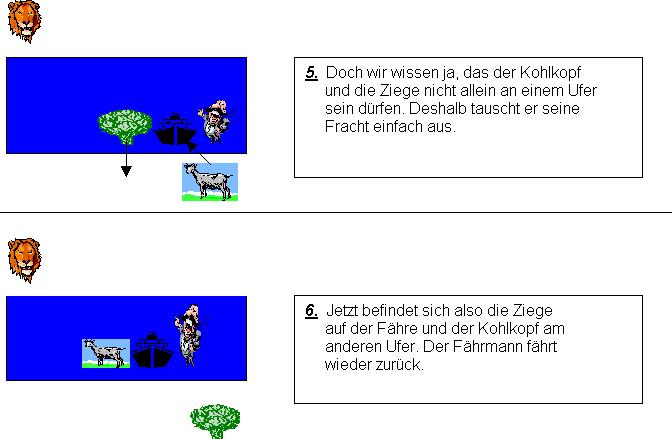
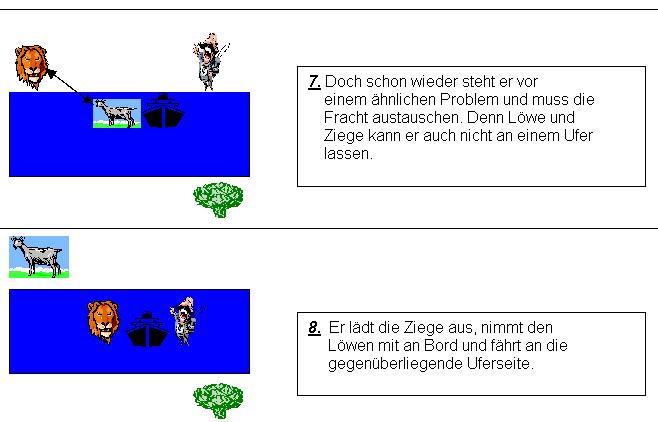
Das war doch eigentlich gar nicht so schwer und ich denke ihr hättet das sicher
auch heraus bekommen :)! Doch jetzt wollen wir an dieses Problem einmal etwas
wissenschaftlicher herantreten und diese Aufgabe mit Hilfe der sogenannten
"Graphentheorie" lösen. Zuerst notieren wir, welche Zustände am Ausgangsufer eintreten
könnten, das heißt welche Möglichkeiten es dafür gibt, dass sich etwas oder jemand
dort befindet. Danach streichen wir die Zustände, die unzulässig sind, weil (hier
oder an der anderen Uferseite) der Löwe die Ziege oder die Ziege den Kohlkopf fressen könnte.
Zu jedem der restlichen Zustände suchen wir alle "Nachbarzustände", das heißt
solche, die durch Abfahrt oder Ankunft des Bootes erreicht werden können, diese
verbinden wir dann miteinander durch eine Linie. Das Bild was sich dann aus Zuständen,
Punkten (= "Knoten" ) und Linien ( = "Kanten") ergibt, stellt einen Graph dar.
Dieser ist zusammenhängend, das heißt, es gibt von jedem Knoten einen Kantenweg
zu jedem anderen Knoten. Um unsere Aufgabe nun zu lösen, müssen wir nur noch
einen Weg vom Knoten 
zum Knoten NICHTS finden. Das ist eigentlich ganz einfach.
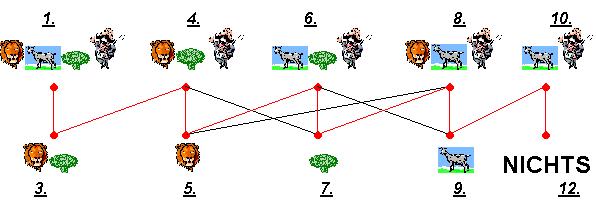
Die Ziffern 1 - 12 stimmen mit meinem vorigen Lösungsweg überein. Zum besseren
Verständnis habe ich meine Lösung durch rote Linien gekennzeichnet. Die anderen
Linien zeigen weitere Lösungsmöglichkeiten. Die Graphentheorie zeigt jedoch nur
die Zustände am Ausgangsufer!
Und, habt ihr immer noch nicht genug? Nein? Dann stürzt euch doch gleich in die
2.Knobelaufgabe !!!
Jetzt fahr'n wir über'n See
Zurück zur Gliederung