2. Faden der Ariadne
Zur Sage:
Kreta war ein Königreich mit einem starken kriegerischem Adel. Der König von Kreta
hieß Minos. Später, als die Griechen kamen, ist der kretische König in die griechische
Sage eingegangen. König Minos hatte einen riesigen und für diese Zeit modernen
Palast, in dem man sich verirren konnte. Die verwirrende Vielfalt der vielen Räume
in dem königlichen Palast ließ die Sage von dem Labyrinth entstehen, das der Athener
Künstler Dädalus gebaut haben soll. In dem Labyrinth wohnte der Sage nach der
Minothauros (griech. = Stier des Minos), ein Fabelwesen mit Menschengestalt und
Tierkopf. Angeblich wurden jedes Jahr sieben Mädchen und sieben Jünglinge von den
Athenern geopfert. Sie wurden dem Ungeheuer zum Fraß vorgeworfen. Der Sage nach
brachte dieser Minotauros auch das Ende von Kreta:
Als Theseus, ein junger griechischer Prinz, nach Knossos gebracht wurde, um dem
Minotaurus geopfert zu werden, erklärte er, unbedingt, bevor er geopfert werde,
mit dem Stiergott reden zu müssen. Dieser Stiergott wohnte in dem Labyrinth, einem
so kunstvoll gebauten Irrgarten, dass nie ein Mensch, der sich da hineinverirrte,
wieder herausfand. Die Priester lächelten hämisch, als Theseus sein Verlangen erklärte,
und der König versprach sich einen Spaß davon. Aber des Königs Töchterlein, die
schöne und lebenslustige Ariadne, verliebte sich Hals über Kopf in diesen blonden
jungen Mann. Als alles vereinbart war, am nächsten Morgen schon sollte Theseus den
Irrgarten betreten und Minotauros darin treffen, kam heimlich Ariadne zu Theseus
und gab ihm einen Wollknäuel, den sollte er abspulen. Es war hellgelbe Wolle, im
hellen Sand unauffällig, damit er aus dem Heckenlabyrinth wieder herausfinde, und
gab ihm das schönste Schwert aus ihres Vaters Waffenkammer. Theseus ging in das
Labyrinth und sah alles, was die Priester vorbereitet hatten, z.B. fürchterliche
Masken mit glühenden Augen, nackte Geier und unheimliche Schlangen. Er sah auch
die Spiegel, die überall so aufgestellt waren, dass Zuschauer seinen Irrweg verfolgen
konnten. Er ging aber keinen Weg zweimal, weil er den Faden der Ariadne hatte, und
gelangte so in das Zentrum und traf dort den abscheulichen Minotauros, einen riesigen
Menschen mit einem grässlichen Stierkopf. Er zog sein Schwert, das kurze kretische
Schwert, das er unter dem Mantel verborgen hatte, und tötete den Gott, rasch, kurz
und schnell, ohne lange Reden, ohne Drohhaltung und Imponierpose! Ohne dem armen
Priester unter seiner Stierkopfmaske auch nur Zeit zu lassen zu erschrecken, stach
er ihn tot!!! Dann nahm er ihm den Stierkopf ab und lief den Faden entlang zurück
zum Ausgang des Labyrinths. Dort hatte sich der König Minos gerade bequem hingesetzt,
um das Schauspiel zu genießen, da war Theseus schon über ihm. Der Held tötete den
König und alle seine Leibwächter, steckte den Palast in Brand und ging hinunter
zum Hafen, wo das Schiff aus Attika noch wartete. Nur eine begleitete ihn, nur
eine lief hinter ihm her mit Pfeil und Bogen, Ariadne, des Königs Tochter. Sie
liebte diesen Fremdling so, dass sie über jeden Kreter jauchzte, den er zu Tode
brachte. Theseus nahm sie mit auf das Schiff nach Attika.
Es gibt viele verschiedene Labyrinthe, große, kleine, verschieden hohe, einfache
und schwierige. Doch eines haben sie alle gemeinsam, jedem Labyrinth kann man einen
Graph zuordnen. Genau, wie wir es in den ersten drei Knobelaufgaben schon getan haben.
Die Knoten stellen jetzt aber die Verzweigungs- und Endpunkte dar
und die Kanten zeigen die Gänge zwischen den Knoten.
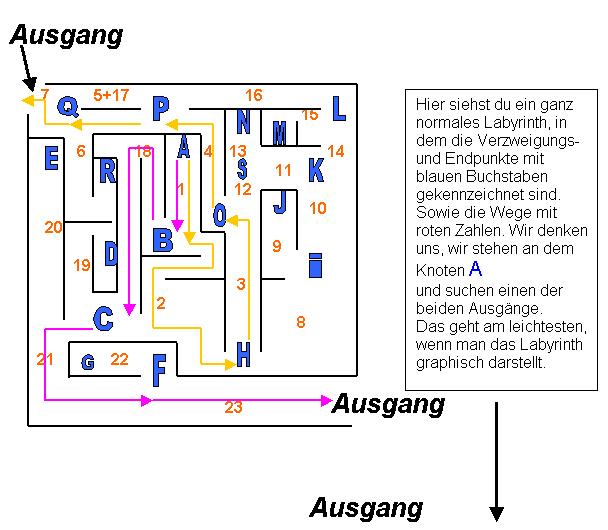
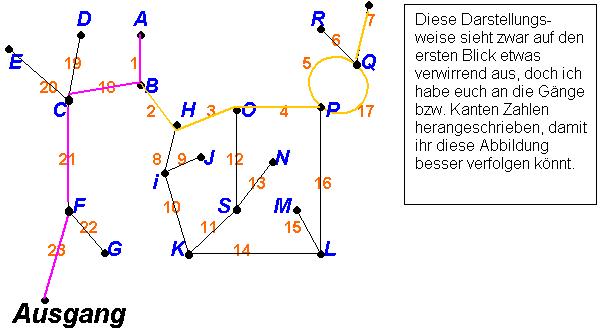
Um den Ausgang eines Labyrinthes zu finden, muss man einen Kantenweg von dem Knoten,
an dem man sich befindet, zum Ausgang erkennen. Das ist einfach, wenn der gesamte
Graph bekannt ist. Wir bilden ihn dann mit einem Fadenmodell nach (wie Graph):
Die Fäden sind die Kanten (z.B. 16), an den Knoten
(z.B. P ) des Graphen werden sie wirklich verknotet. Fassen wir von jedem Knoten, von dem aus wir den Ausgang
suchen, und am "Ausgangsknoten" an und ziehen sie auseinander, so sind die Fadenstücke
die Kanten eines Weges zum Ausgang.
In den oberen Darstellungen sind die beiden kürzesten Wege zum jeweiligen Ausgang
farbig gekennzeichnet. Dies sind die Fäden der jeweiligen Kanten. Meine Aufgabe
war es vom Knoten A aus die kürzesten Kantenwege zu den Ausgängen zu finden. Mein
erster Weg trifft die Punkte: A, B, C, F und der zweite die Knoten: A, B, H, O, P, Q.
Und die Fäden verlaufen auf den Wegen: 1, 18, 21, 23 und auf den Kanten 1, 2, 3, 4, 5, 7.
Dieser Einblick soll für das erste reichen.
Doch nun stellt euch aber einmal vor, ihr befändet euch inmitten eines euch
unbekannten Labyrinthes, ohne dessen Plan mit eingezeichnetem eigenen Standort zu
besitzen. Was tun? Oft kommt man auch mit der "Rechte - Hand - Regel" zum Ausgang.
Diese lautet: Gehe, wenn du auf eine Verzweigung triffst (Knoten), den am weitesten
rechts liegenden Weg (Kante) weiter!
Diese Regel ist oft sehr nützlich, versuche einmal auf diese Weise, das obere
Labyrinth vom Ausgangspunkt A zu verlassen.
Du hast sicher gemerkt das dies ganz einfach über die Knoten A, B, C, D, C, E, C, F
und die Kanten 1, 18, 19, 19, 20, 20, 21, 23 gelingt. Dieser Weg ist zwar etwas
umständlich, aber immer hin kommt man zu dem Ausgang.
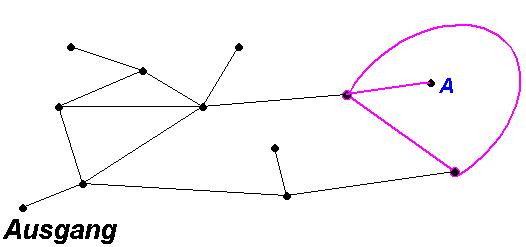
Leider hilft diese Regel aber nicht immer. Das nächste Labyrinth, kannst du von
Knoten A aus auf diese Weise nicht verlassen.
Du würdest nur auf den rosafarbenen Wegen (Kanten) herumlaufen und den Ausgang
niemals finden. Das geschieht durch den eingebauten Halbkreis im Labyrinth und
dadurch, dass der Punkt A in ihm liegt.
Wenn wir den Ausgang finden wollen, müssen wir alle Gänge nach ihm absuchen. Bis
wir ihn gefunden haben. Gesucht ist also eine Methode, die - ohne dass wir das
Labyrinth kennen - uns durch die Gänge führt, ohne einen zu vergessen.
Wenn ihr wissen wollt wie diese Methode funktioniert, dann schaut doch einfach mal
in der Seite "Algorithmus von TREMAUX" nach. Es wird euch sicher gefallen :)!
Jetzt fahr'n wir über'n See
Zurück zur Gliederung
