7.2. Bézier-Kurven

	Die von dem franz. Mathematiker P. Bézier entwickelte Möglichkeit, eine beliebige n-dimaensionale Kurve durch n+1 Punkte zu definieren. Die von  Bézier entwickelte Technik ist eine Vorform der Spline-Technik, die für die Entwicklung und Beschreibung beliebig gekrümmter Oberflächenformen, vor allem im rechnerunterstützten Entwurf, große Bedeutung erlangt hat. Bézier-Flächen haben komplizierte Oberflächenformen, die nicht mit den analytischen Methoden der Kegelschnitte beschrieben werden können. Sie werden mit Hilfe dreidimensionaler Darstellungen, die auf Polynomen beruhen, abgebildet. Vor allem im Flugzeug- und Automobilbau wird diese Technik heute vielfach verwendet. B-Splines ... sind Verfahren der Interpolation zur Darstellung von Funktionen höheren Grades. Dabei wird eine Funktion n-ten Grades durch n+1 Punkte definiert. Die auf diese Weise erzeugten Kurven werden als Spline-Kurven bezeichnet. Es handelt sich um eine Form der Approximation, die vor allem im Bereich der numerischen Steuerung von Werkzeugmaschinen und in der grafischen Datenverarbeitung angewendet wird.
	1. Bézier-Kurven und B-Splines 2. Erstellen einer Bézier-Kurve 3. Bearbeiten einer Bézier-Kurve 4. Einsatzmöglichkeiten der Béziers 5. Einsatzbeispiele 6. Tipps'n Tricks zur Knotenbearbeitung
	Bevor das eigentliche Setzen beginnen kann, soll zunächst die Satzumgebung mit ihren Elementen, Fenstern und Funktionen beschrieben werden.

1. Bézier-Kurven und B-Splines

	zu jedem Knoten (außer zum Anfangsknoten) gibt es einen korrespondierenden Abschnitt (das Kurvenstück vor dem Knoten!!!)
	Markierung eines Knotens bewirkt dessen Markierung und Einblendung der Kontrollpunkte des markierten Knotens sowie jeweils eines Kontrollpunktes der beiden benachbarten, wenn vorhanden
	Markierung mehrerer Knotens bewirkt ausschließlich deren Markierung ohne Einblendung der Kontrollpunkte - sie wird durch Markieren bei gedrückter SHIFT-Taste bewirkt
	SHIFT- und CTRL-Taste gedrückt bewirkt die Markierung aller Knoten einer Kurve

nur den Anfangsknoten markiert man durch HOME-Taste, wohingegen der Endknoten mit der END-Taste erreichbar ist

2. Erstellen einer Bézier-Kurve

Hilfsmittel "Bézier" aufrufen	Werkzeugpalette nach dem Umschalten auf das Hilfsmittel "Bézier"	mit gedrückter linkeer Maustaste Linie ziehen
mit Klick linke Maustaste Operation abschließen

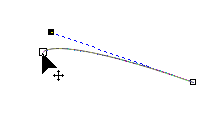
	bewirkt eine Veränderung der Form und der Länge der beiden benachbarten Abschnitte
	die Krümmung der Kurve wird dabei konstant gehalten
	nur wenn mehrere Knoten verschoben werden, so bleibt der Abstand zwischen diesen unverändert

mit gedrückter CTRL-Taste werden markierte Konten nur horizontal oder vertikal verschoben

3. Kontrollpunkte verschieben

Beziér-Linie

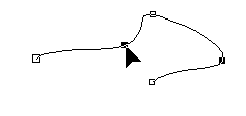
	eine Verlagerung der Kontrollpunkte ergibt eine mathematisch beschreibbare Veränderung des Verlaufes der Kurve
	nichtsichtbare Kontrollpunkte erreicht man kein Knoten darf markiert sein SHIFT-Taste drücken Kontrollpunkt unter dem Knoten „hervorziehen“

	Veränderung des Winkels des Kontrollpunktes beeinflusst den Kurvenverlauf
	mit gedrückter CTRL-Taste wird der markierte Kontrollpunkt nur horizontal oder vertikal verschoben
	der Abstand des Kontrollpunktes zum zugehörigen Knoten beeinflusst proportional die Krümmung der Kurve

4. Einsatzmöglichkeiten der Béziers

	Bézier-Kurven lassen sich besonders vorteilhaft im Zusammenwirken mit  Power-Lines einsetzen
	wenn man einen der Kontrollpunkte verschiebt, ändert auch der zweite seine Lage, d. h. die Kurve verläuft an einem glatten Knoten stetig (enthält keinen „Knick“)

Symmetrische Knoten

wie glatte Knoten mit dem Zusatz, dass beide Kontrollpunkte den gleichen Abstand vom Knoten haben

Spitze Knoten

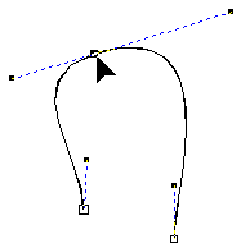linker Knoten glatt

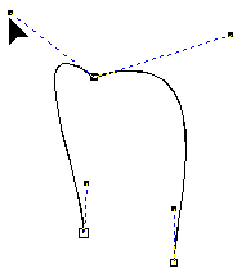Kontrollpunkt nach oben gezogen

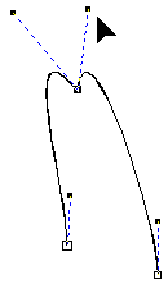zusätzlich rechter Kontrollpunkt gezogen

	die Kontrollpunkte und Knoten liegen nicht zwangsläufig auf einer Geraden
	die Kontrollpunkte lassen sich unabhängig voneinander bewegen
	eine Kurve mit spitzen Knoten muss nicht stetig sein, kann aber, wenn dies durch Knotenbearbeitung erzwungen wurde

5. Knotenbearbeitung

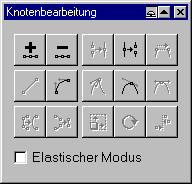
Das Popup-Menü Knotenbearbeitung

Kombination von Knoten
Knoten-Kombination aufheben
Knoten einfügen
Knoten löschen

	Der Quelltexteditor "versteckt" sich beim Start von Delphi zunächst hinter dem Formularfenster, so dass wir ihn erst einmal in den Vordergrund rücken müssen.
	Im Quelltexteditor erfolgt das eigentliche Programmieren. Obwohl Delphi ursprünglich auf der Programmiersprache Turbo Pascal basiert, ist es aber inzwischen weit mehr als das.
	Der Quelltext (Quellcode) enthält die Befehle (Anweisungen), die dann während der Programmausführung abgearbeitet werden.
	Man erkennt hier bereits einige Befehlszeilen, die von Delphi selbst eingetragen werden.

6. Tipps'n Tricks zur Knotenbearbeitung

Das Popup-Menü Knotenbearbeitung

Kombination von Knoten
Knoten-Kombination aufheben
Knoten einfügen
Knoten löschen

	Der Quelltexteditor "versteckt" sich beim Start von Delphi zunächst hinter dem Formularfenster, so dass wir ihn erst einmal in den Vordergrund rücken müssen.
	Im Quelltexteditor erfolgt das eigentliche Programmieren. Obwohl Delphi ursprünglich auf der Programmiersprache Turbo Pascal basiert, ist es aber inzwischen weit mehr als das.
	Der Quelltext (Quellcode) enthält die Befehle (Anweisungen), die dann während der Programmausführung abgearbeitet werden.
	Man erkennt hier bereits einige Befehlszeilen, die von Delphi selbst eingetragen werden.